Freely Available British and Irish Public Legal Information
[Home] [Databases] [World Law] [Multidatabase Search] [Help] [Feedback]
England and Wales High Court (Patents Court) Decisions
You are here: BAILII >> Databases >> England and Wales High Court (Patents Court) Decisions >> Optis Cellular Technology LLC & Ors v Apple Retail UK Ltd & Ors [2021] EWHC 3121 (Pat) (25 November 2021)
URL: http://www.bailii.org/ew/cases/EWHC/Patents/2021/3121.html
Cite as: [2021] EWHC 3121 (Pat)
[New search] [Printable PDF version] [Help]
Neutral Citation Number: [2021] EWHC 3121 (Pat)
Case No. HP-2019-000006
IN THE HIGH COURT OF JUSTICE
BUSINESS AND PROPERTY COURTS OF ENGLAND AND WALES
INTELLECTUAL PROPERTY LIST (ChD)
PATENTS COURT
Rolls Building
Fetter Lane
London, EC4A 1NL
November 25th 2021
Before :
MR JUSTICE MEADE
- - - - - - - - - - - - - - - - - - - - -
Between :
|
|
(1) OPTIS CELLULAR TECHNOLOGY LLC (2) OPTIS WIRELESS TECHNOLOGY LLC (3) UNWIRED PLANET INTERNATIONAL LIMITED |
Claimants
|
|
|
- and - |
|
|
|
(1) APPLE RETAIL UK LIMITED (2) APPLE DISTRIBUTION INTERNATIONAL LIMITED (3) APPLE INC
|
Defendants
|
James Abrahams QC, James Whyte and Michael Conway (instructed by EIP Europe LLP and Osborne Clarke LLP) for the Claimants
Lindsay Lane QC and Adam Gamsa (instructed by WilmerHale LLP) for the Defendants
Hearing dates: 5-7 and 13-14 October 2021
- - - - - - - - - - - - - - - - - - - - -
Covid-19 Protocol: This Judgment was handed down remotely by circulation to the parties’ representatives by email and release to Bailii. The date for hand-down is deemed to be 25 November 2021.
Mr Justice Meade:
Optis’ expert, Ms Johanna Dwyer 5
Apple’s expert, Prof Angel Lozano. 7
The common general knowledge. 10
Agreed common general knowledge. 11
Background to LTE and RAN1. 11
Division of radio resources within a cellular network. 11
User data and control information. 13
Resource allocation in LTE.. 14
Other downlink physical channels in the control region. 17
Transmitting Downlink Control Information (DCI) on PDCCH.. 18
Search spaces and blind decoding of PDCCHs. 18
Knowledge of hashing functions and random number generation. 19
Technical Background - Collisions and Blocking. 20
Disputed common general knowledge. 22
Hashing functions v random number generators. 24
Recursive v. self-contained. 25
Claims of the Patent in issue. 28
Prejudice/lion in the path. 35
Technograph and number of steps. 36
Pozzoli question 4 - unspecified claims. 37
Assessment of the Ericsson function. 38
A specific point on mod C.. 48
Same parameters for all aggregation levels. 50
Assessment of the secondary evidence. 50
Alternative routes - overall assessment 53
Conclusion on obviousness of the unspecified claims from Ericsson. 54
Obviousness of the specified claims. 54
Insufficiency of the unspecified claims. 58
Introduction
1. This is “Trial C” in these proceedings. Trials A, B and F have already taken place and the parties and the general shape of the litigation need no further introduction.
2. There are three patents in issue at this trial, namely EP (UK) 2 093 953 B1, EP (UK) 2 464 065 B1 and EP (UK) 2 592 779 B1 (“the Patents”). They are all closely related and from the same family, and it is common ground that I can decide all the issues by consideration of claims 1 and 4 of EP (UK) 2 093 953 B1. I will refer to it hereafter as “the Patent” and references to paragraph numbers are to the paragraph numbers in its specification.
3. The Patent was originally applied for by LG Electronics Inc (“LGE”). Optis is the assignee. The Patent is declared essential to LTE. By the time of the PTR, Apple had conceded that the Patent is indeed essential and therefore infringed if valid. The concession was said to be for reasons of “procedural economy”; whether that was the actual motivation is irrelevant to this judgment.
4. Essentiality having been conceded, the issues at trial were in relation to validity only. At the PTR I directed, after argument, that Apple should open the case and call its evidence first.
Conduct of the trial
5. The trial was conducted in Court. All the oral evidence was given live. To mitigate the COVID risk, the number of representatives of the parties and their clients permitted at any one time was limited, and a live feed was made available for others, and for the public should they ask. I am grateful to the third-party providers engaged by the parties to make the technology work.
6. Mr Abrahams QC, Mr Whyte and Mr Conway appeared for Optis and Ms Lane QC and Mr Gamsa for Apple.
The issues
7. The remaining issues were:
i) The nature of the skilled person, where there was a major disagreement, although in the end I do not think it matters to my overall conclusion.
ii) The scope of the common general knowledge (“CGK”). There was significant dispute here too.
iii) Obviousness over Slides R1-081101 entitled “PDCCH Blind Decoding - Outcome of offline discussions” presented at a RAN1 meeting of 11-15 February 2008 (“Ericsson”), in conjunction with CGK.
iv) Obviousness over The Art of Computer Programming, Vol. 2 Seminumerical Algorithms, 2nd Ed (1981), Chapter 3 “Random Numbers”, pages 1-40 (“Knuth”) in conjunction with CGK.
v) The significance or otherwise of the secondary evidence of how RAN1 members were working at the time and how they reacted to Ericsson and to the alleged invention of the Patents.
vi) Two insufficiencies, run primarily as squeezes against obviousness (although Apple said that at least claim 1 was both obvious and insufficient).
8. Apple argued that both Ericsson and Knuth were CGK (or such that each would be found by routine research - see below), and its obviousness cases were essentially from Ericsson as a starting point and thence to Knuth, or from Knuth as a starting point and thence to Ericsson. The former was its primary case; the latter depended on a narrow definition of the skilled person so as to make Ericsson CGK. I return to this in more detail below.
9. In closing written submissions, Apple indicated that it wanted to reserve the right to argue that it ought to be entitled to mosaic Ericsson and Knuth even if neither was CGK and, as I understood the submission, the one would not be found by obvious research from the other. The basis for this submission was that UK law is out of step with the European Patent Office (“EPO”), and that in the EPO such a mosaic would be allowed by virtue of the problem-solution analysis. I merely note this indication; I was not asked to decide the argument or even to rule on whether it would be open to Apple to run it at all at such a late stage.
The witnesses
10. Each side called one expert witness. There was no fact evidence.
Optis’ expert, Ms Johanna Dwyer
11. Optis’ expert was Ms Johanna Dwyer. She gave evidence in Trial B as well, on which occasion she spoke to how ETSI worked and how its IPR Policy had developed. In my judgment on that Trial I described her career as follows:
“She worked for RIM/Blackberry for many years, and from 2005 until 2012 she was involved in various aspects of standards and IP. She participated in various 3GPP WGs and TSGs. She worked on IPR declarations and held senior positions in relation to system standards. Following an MBA in 2012 she has worked in more business-focused and consultancy roles, still very largely in cellular communications. She has given evidence in the Eastern District of Texas proceedings between the parties.”
12. Apple sought to suggest that Ms Dwyer was, by the priority date, not really engaged in technical work at all, but only on IP matters. This was based on the way she expressed things in her CV. I reject this criticism. Ms Dwyer plainly had and has very considerable technical expertise in telecoms. Her CV is a short one which she said was typical for Canada, where she lives, and did not seem to have been prepared for this or any other litigation, but to obtain work for her business. It therefore emphasises IP, since that is the expertise she now focuses on.
13. However, although that criticism was misplaced, Apple made much more headway in relation to whether Ms Dwyer’s technical knowledge and experience put her in a good position to give evidence on the specific issues in this case. I thought the following were important:
i) Ms Dwyer did not have any real, specific experience of RAN1. She was not an attendee of any meetings and she did not send any RAN1 emails (of which a repository exists).
ii) She had never done any RAN1 simulations and she was forbidden by Optis’ advisers from doing any for this litigation.
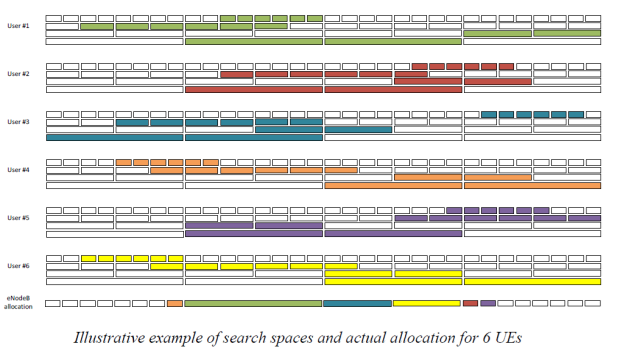
iii) She was not experienced with modular arithmetic. She had no practical experience before this litigation and had to look it up. She could not remember if she studied it at university.
iv) She made errors in modular arithmetic in her written evidence. Of course typographical errors happen to everyone and do not in themselves reflect on a witness, but she corrected one particular error without noticing that exactly the same mistake was repeated multiple times over adjacent pages.
v) She actively put forward ideas based on modular arithmetic which were wrong. In particular, she put forward two ways to turn the Ericsson function into an LCG which were wrong, the first being meaningless and the second still suffering from the C=16 problem in Ericsson (I explain below what these mean).
vi) She had a conception of what aspects of modular arithmetic would be CGK (or be found readily by the skilled person) which I found hard to make sense of: she said that the modulo function (which is just derivation of a remainder) would be CGK but that the distributive property of modular arithmetic (again explained below) would not. The latter is necessary to be able to see one of the problems with Ericsson, but it is not really very complicated.
14. Ultimately Ms Dwyer accepted that if the skilled person were someone that understands modular arithmetic to a greater degree than her, then she could not assist the Court with what the skilled person would do with a function that has modular arithmetic in it.
15. Ms Dwyer’s unfamiliarity with (1) RAN1, (2) simulations relevant to RAN1 and (3) modular arithmetic lead me to conclude that her evidence is of extremely limited help on the key issues in this case.
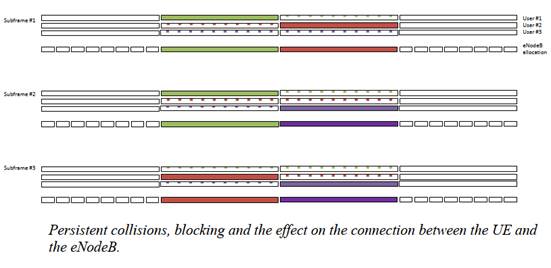
16. I also think that Ms Dwyer put far too much emphasis on the secondary evidence. Her first report, for example, had 49 pages about it. Often, both in written and oral evidence, she would address what the skilled person would do or think first and foremost by reference to what a specific person in RAN1 had done or said, without adequate caution about whether that person was representative of the skilled person, and without really addressing what the notional skilled person would do, or think.
17. None of this is to criticise in any way Ms Dwyer’s integrity or independence. Her answers were clear and direct and she did not, for example, try to avoid recognising where she lacked of familiarity, or her mistakes. I remain of the view that I formed in Trial B that she is a very good expert in terms of her personal qualities. It is just that in this trial she was materially outside her area of expertise.
Apple’s expert, Prof Angel Lozano
18. Apple called Prof Angel Lozano. He is currently an academic, being a Full Professor at Universitat Pompeu Fabra. Following his doctorate in 1999 he was until 2008 a researcher at Bell Labs working on various wireless communications issues. In parallel he was an adjunct professor at Columbia University. From about 2006 he was commissioned to support the standardisation team of Lucent, Bell’s parent (later acquired by Nokia). As part of that he attended various 3GPP meetings as a RAN1 delegate in 2006/2007.
19. Apple thought that Optis was criticising Prof Lozano for being too academic, lacking real world experience. I do not think Optis was saying this, and if it was then it was unsustainable given his direct exposure to RAN1 meetings while working in industry at exactly the priority date.
20. Optis did say that Prof Lozano was afflicted by hindsight because he knew of the alleged invention from his real-world experience. I reject this. He merely said that he had some “minimum” familiarity with the PDCCH search space.
21. Optis also said that Prof Lozano was affected by hindsight in relation to the case of obviousness over Knuth because he approached it on the assumption that the reader knew about the problem to which the Patents are addressed in terms of PDCCH search space. I tend to agree with this and it is consistent with my reasons for rejecting the obviousness case starting from Knuth, but it is not relevant to the argument starting from Ericsson and there I think the professor’s approach was entirely appropriate.
22. Optis went on to make various more specific points which are addressed below. I did not think there was anything in them.
23. I found Prof Lozano overall to be an excellent witness. He was very clear in his explanations and short and direct in his answers on the whole. He had a practical approach too, as evidenced by the fact that in relation to some aspects of Knuth he said that the skilled person would not find it necessary to grapple with all the details of dense mathematical proofs but would instead undertake some simulations.
24. Prof Lozano was familiar with simulations and I think his approach to them was in line with what RAN1 workers would have done.
25. Overall therefore I found Prof Lozano a much more cogent witness than Ms Dwyer. Naturally, that does not mean that I should accept anything he said uncritically. In places, Counsel for Optis made some progress during a careful, detailed and sustained cross-examination, the attack starting from Knuth being the main one. But in general, where the issues are ones of balancing his views against those of Ms Dwyer, and in areas where the cross-examination did not dent his position, I prefer his evidence to Ms Dwyer’s on the basis that he was much better placed to explain what the skilled person would think, and to put himself in that person’s position.
26. I should say that this is not the same thing as trying to decide which of two well-qualified experts is in fact the closest approximation to the notional skilled person. That is not a legitimate way to approach patent cases. My findings are instead based on Prof Lozano being so much better able to put himself in the position of the skilled person by virtue of greater real-world familiarity and, rarely for a patent case, on Ms Dwyer lacking the minimum necessary understanding of the technical issues to be able to perform the same task. Prof Lozano also gave a much more appropriate degree of consideration to the secondary evidence.
27. Finally in relation to the experts, I should mention that Optis said that simulations that Prof Lozano had done for his reports were experiments and ought not to be permitted. Optis did not seek to have them excluded at the PTR, however, and instead took the approach that while they ought not to be excluded altogether they did not deserve to be given any weight. I reject this; Optis’ chance to have them excluded passed and if it wanted to undermine their weight then they should have been addressed during cross-examination, which they were not. However, their significance to my decision is modest.
The skilled person
28. Optis said that the skilled person would be a person engaged in work on RAN1. Apple said that the skilled person would be a person engaged in the more narrow field of the PDCCH specifically.
29. I considered the applicable law recently in Alcon v. Actavis [2021] EWHC 1026 (Pat), drawing heavily on the decision of Birss J, as he then was, in Illumina v. Latvia [2021] EWHC 57 (Pat). The particularly relevant passages are [68]-[70] in Illumina and [31] in Alcon.
30. At [68] in Illumina Birss J provided the following approach:
“68. I conclude that in a case in which it is necessary to define the skilled person for the purposes of obviousness in a different way from the skilled person to whom the patent is addressed, the approach to take, bringing Schlumberger and Medimmune together, is:
i) To start by asking what problem does the invention aim to solve?
ii) That leads one in turn to consider what the established field which existed was, in which the problem in fact can be located.
iii) It is the notional person or team in that established field which is the relevant team making up the person skilled in the art.”
31. And in Alcon at [31] I said:
“31. I intend to apply that approach. I take particular note of:
i) The requirements not to be unfair to the patentee by allowing an artificially narrow definition, or unfair to the public (and the defendant) by going so broad as to “dilute” the CGK. Thus, as Counsel for Alcon accepted, there is an element of value judgment in the assessment.
ii) The fact that I must consider the real situation at the priority date, and in particular what teams existed.
iii) The need to look for an ‘established field’, which might be a research field or a field of manufacture.
iv) The starting point is the identification of the problem that the invention aims to solve.”
32. In the present case, the problem that the invention aims to solve is not in dispute: it is a narrow one of how to allocate PDCCH search spaces.
33. The established field in which this problem was in fact located was RAN1. The PDCCH was not a field in its own right. Prof Lozano accepted that no one would have had a scope of work that matched it. It was too narrow for that. There was no RAN1 sub-group or sub-plenary devoted to it.
34. Thus I reject Apple’s argument that the skilled person would have been a PDCCH person in the sense Apple meant that. It is a “blue Venezuelan razor blade” kind of argument (see [62] in Illumina), though not nearly as extreme in degree as that imaginary example.
35. Optis’ view of the skilled person has the benefit that RAN1 clearly was an established field, and that the problem that the invention aims to solve is within its scope.
36. However, in my view Optis treated the analysis that the skilled person is a RAN1 person as an opportunity to carry out some inappropriate dumbing-down through dilution, of the kind deprecated in Mayne v. Debiopharm [2006] EWHC 1123 (Pat) and cited by Birss J in Illumina and recognised by me in Alcon. RAN1 is a broad umbrella and probably no one real person had the knowledge, skills and experience to cover the whole of its field. One can see that by the number of people participating in the discussions, and by the fact that major companies had teams on RAN1, either attending as delegates or participating in the background.
37. Where this is of potential practical importance in the present case is in Optis’ contentions that the skilled person would not be comfortable with, for example and in particular, modular arithmetic, or hashing functions/random numbers. This was basically a submission that the skilled person would lack the basic tools to do the task which Ericsson set - to assess its function and then improve it if necessary. The submission was rather grounded in the idea of the skilled person being an individual spread so thin across RAN1 that their CGK on any particular aspect of it must be very shallow. For the reasons I have just given, I reject this as a matter of principle and on the facts.
38. My conclusion in this respect is supported by the principle expressed by Pumfrey J in Horne v. Reliance [2000] FSR 90 (also cited in Illumina) that the attributes of the skilled person may often be deduced from assumptions which the specification clearly makes about their abilities. In the present case the specification of the Patents gives the skilled person some parameters for use as A, B and D in the LCG of the claims, but it assumes that with only the modest amount of help that the specification gives, the skilled person would be able to find more options for the parameters if they wanted to.
39. Thus I conclude that the skilled person in this case is a “RAN1 person” of the kind attending meetings or providing back-up, with the aptitudes and CGK appropriate to the tasks that RAN1 would require of them. In real life, as I say, the organisations involved will have had multiple people to give this coverage, but in the present case I can refer in the singular to “the skilled person”.
40. While the “dilution” point is of potential general importance, the RAN1 v PDCCH point only matters for the case over Knuth, since Optis accepts that the RAN1 skilled person starting from Ericsson would know or look up the material relied on by Apple.
The common general knowledge
41. There was no dispute as to the applicable legal principles: to form part of the CGK, information must be generally known in the art, and regarded as a good basis for future action. It is not a requirement for CGK that the skilled person would have memorised it; CGK includes information that the skilled person would refer to as a matter of course.
42. In relation to obviousness, the Court also may have regard to information which the skilled person would acquire as a matter of routine if working on the problem in question. Information of that kind is not CGK as such (although the effect may be very similar) but rather may be taken into account because it is obvious to get it. See KCI v. Smith & Nephew [2010] EWHC 1487 (Pat) at [108]-[112], approved on appeal at [2010] ECWA Civ 1260.
43. As is now usual, the parties submitted a document setting out the agreed matters of CGK, which I have used as the basis for the next section of this judgment. Where I have removed material it is because I think it of low relevance, not because I disagree with it.
44. The section on “Collisions and Blocking” was produced during trial after I asked what the position was on the state of CGK on that topic. Its contents are not accepted by Optis as being CGK because Optis (successfully) disputed that the skilled person is a PDCCH person (see above), but Optis does accept that its contents would be “apparent” to a RAN1 person reading Ericsson or “otherwise tasked specifically with the problem of control signalling on the PDCCH”.
45. I take this to mean that the contents of the section can by agreement be treated as CGK for the practical purposes of the case starting from Ericsson, and that is how the argument proceeded. In some cases it could be important that information found by routine research would not be known to the skilled person right at the outset of their consideration of the prior art, but only after they had identified a problem. But in the present case the skilled person would acquire the information about collisions and blocking straight away, since it is necessary to understanding Ericsson.
46. There was also a dispute about the relevant sources of CGK. Usually, CGK is proved by means of well-established textbooks and the like. In this field there was no textbook specific to LTE. But in any event, the dispute was really about the path from Ericsson to Knuth, and I deal with it in the context of obviousness. At this stage I merely observe that what one is considering is whether particular information was CGK; it is legitimate for a party to put forward materials as examples of how information would be obtained, without necessarily saying that those materials are themselves CGK.
Agreed common general knowledge
Background to LTE and RAN1
47. LTE stands for “Long Term Evolution” and is (or at least became) a “fourth generation” (4G) Radio Access Network (RAN). It succeeded the second and third generation systems (2G and 3G). It was driven by EU, US, Chinese, Japanese, South Korean and (to some extent) Indian initiatives.
48. In 3GPP, Technical Specification Group (TSG) RAN Working Group 1 (RAN1) is responsible for the physical layer (L1) specifications.
49. There was no actual LTE network at the Priority Date (19 February 2008). The first technical specifications defining LTE were published in 2007 as part of Release 8, which was the Release current at the Priority Date.
Division of radio resources within a cellular network
50. In a cellular communications system, a “resource” is a term used to refer to the way in which the radio spectrum is divided up and allocated so that different transmissions can be distinguished from one another. Resources can be defined in different ways, such as by a given period of time, at a particular frequency, or using particular codes.
51. In LTE, as with other cellular systems, the radio resource is divided between resources used for transmissions from UEs (i.e. mobiles) to the eNodeB (i.e. base station), which is referred to as the “uplink”, and resources used for transmissions from the eNodeB to UEs, referred to as the “downlink”.
52. In addition to the division between uplink and downlink transmissions, cellular networks also need a way of allocating resources between transmissions from and to different UEs, and between transmissions on different channels (e.g., those for sending control information or user data). These techniques are referred to as multiple access technologies.
Protocols and Layers
53. A common way of conceptualizing mobile communications systems is the Open Systems Interconnection (OSI) model. The OSI model divides the processes by which data is transmitted and received into different protocol ‘layers’, in which each layer relates to particular functionality. A group of layers that communicate with each other to transmit and receive data is referred to as a protocol “stack”. When transmitting, data packets are passed from higher layers in the stack down to lower layers.
54. At each layer, data is operated on according to the protocols specified for that layer, e.g., header information may be added or removed, or data packets combined or separated, before being passed up or down the stack to the next layer. Each layer in the transmitting entity can be thought of as being in logical communication with its peer in the receiving entity.
55. A simplified version of the protocol layer architecture within LTE is shown in Figure 2 below.
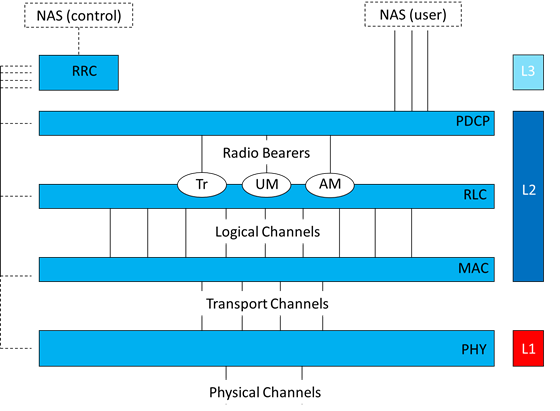
Figure 2: Protocol layer architecture within LTE
56. Layer 1 (L1) is the Physical Layer (or PHY) which is responsible for the processes required to prepare data for transmission and transmitting it over the air interface (and on the receiving side, converting radio signals into digital format for passing up to higher layers).
57. Layer 2 (L2) is the data link layer. It comprises the Packet Data Convergence Protocol (PDCP), Radio Link Control (RLC) and the Medium Access Control (MAC) sub layers. In broad terms, Layer 2 is responsible for managing the flow of information between the UE and the Access Network. This involves, for example, data compression and decompression, combining and segmenting data packets, error detection and retransmission of data, resource management, and determining a suitable transport format to pass data on to the PHY.
58. Layer 3 (L3) is the network layer. This comprises the Radio Resource Control (RRC). The RRC is broadly responsible for the signaling required to set up, configure and take down connections between the UE and the network and for managing the protocols to be applied to different services.
User data and control information
59. Two types of information may be transmitted up and down the stack and over the air: namely, user plane data and control plane information. User plane data refers to data transferred between an application and its peer application at the other end of an end-to-end connection (e.g., voice or packet data between two mobile users). Control plane information comprises messages used to configure and manage the network, such as signaling to indicate whether a packet has been received accurately, or scheduling information.
Channels and PDCCH
60. A “channel” refers to a communication pathway used for a specific purpose or for sending information of a particular type, such as certain kinds of control information, or user data. Data sent on a given channel is configured in a particular way according to a set of rules specified by the standard.
61. In LTE, what defines a channel also depends on the level in the protocol stack. Between the RLC and MAC, “logical channels” are used to carry information for certain purposes. At the MAC layer, two or more logical channels may then be combined into a single “transport channel”, for onward transmission to the physical layer.
62. At the physical layer, transport channels are mapped to “physical channels”, which are configured to have a particular structure and to use a particular set of resources. LTE has some physical control channels which carry signaling necessary to configure transmissions on the physical layer, such as resource allocations. In the downlink, these include the PDCCH in LTE, described in more detail below. The PDCCH is one of seven different channel types that can carry control information. PDCCH may refer to a specific single control channel between the eNodeB and an individual UE, or refer to all PDCCH channels.
Resource allocation in LTE
63. Multiple possible channel bandwidths can be used in LTE, which are: 1.4 MHz, 3 MHz, 5 MHz, 10 MHz, 15 MHz, and 20 MHz. The channel bandwidth limits the resources available.
64. In LTE, radio resources are divided up according to a two-dimensional resource space in the time and frequency domains:
i) In the time domain, LTE uses units of 10 ms called a radio frame, where each radio frame is further divided into ten 1 ms subframes. Each 1 ms subframe is further divided into two “slots” of 0.5 ms duration.
ii) In the frequency domain, the overall bandwidth is divided up into a number of evenly spaced narrow frequency bands called subcarriers. Data subcarriers in LTE span 15 kHz regardless of the channel bandwidth. The symbol time is the inverse of the subcarrier spacing, therefore the symbol time in LTE is 66.67 µs.
65. Resources in LTE are allocated in units called Resource Blocks (RBs). Each RB comprises one slot in time and spans twelve 15 kHz subcarriers in the frequency domain (180 kHz). In the time domain, each slot is divided into either six or seven OFDM symbols, depending on how it is configured, each of which spans the 12 subcarriers of the RB (Six symbols are used when the RB is configured to use a technique referred to as “extended cyclic prefix”. It is not necessary to describe this any further for the purposes of the issues in this case). An illustration of the resource grid in the downlink showing a resource block with seven symbols is shown in Figure 3, which is extracted from TS 36.211 (as Figure 6.2.2-1).
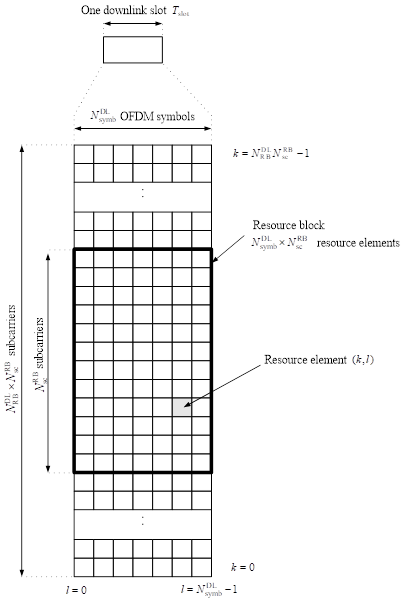
Figure 3: Downlink resource grid as depicted in Figure 6.2.2-1 of TS 36.211
66. As shown in Figure 3, the smallest unit in time and frequency is a Resource Element (RE), which consists of a single subcarrier in frequency and a single symbol in duration (time).
67. Within a given subframe (comprising two slots), some REs may be used for data (uplink or downlink) whereas other REs are reserved for particular purposes, for example control channels, broadcast channels, indicator channels, reference signals and synchronization signals. Depending on their location, these reserved portions of the subframe have an impact on the REs available for downlink or uplink data transmissions in a given RB, and on the total REs available for downlink control information.
Scheduling
68. LTE makes use of shared (amongst multiple UE) physical channels for both data and control signaling in the downlink and the uplink. The resource allocation provided in control messages from the eNodeB to the UEs within a cell indicates the resources in the downlink channel that contain downlink transmissions for a given UE, and which resources in the uplink channel are assigned to a given UE to make uplink transmissions. The choice of which resources are assigned to which UE is called “scheduling” and is managed by the eNodeB. The minimum resource unit for scheduling purposes is one RB. In addition to the resource allocation, the eNodeB specifies the parameters of the data transmissions sent in each scheduled RB. In LTE, this control signaling is handled in the physical layer.
69. Explicit control signaling indicating to the UE where to find the downlink data intended for it and the relevant parameters needed to successfully decode that downlink data avoids considerable additional complexity which would arise if UEs had to search for their data on the Physical Downlink Shared Channel (PDSCH) amongst all possible combinations of resource allocation, packet data size, and modulation and coding schemes.
70. When making scheduling decisions, the eNodeB takes into account various considerations, such as the amount of downlink data it needs to transmit to each UE, the amount of data each UE has to send in its uplink buffer, the quality of service requirements of that data, the signal quality for each UE, and what antennas are available. The scheduling algorithms used by eNodeBs are not specified in the standard and are left to the implementation.
Downlink control in LTE
72. The DCI is sent in PDCCHs in the control region at the start of the downlink subframe. The DCI contains critical information for the UE, because it informs the UE about its uplink resource allocation and where to find its information on the downlink. The control region may span from 1 to 3 symbols.
73. The design of the PDCCH included the UE procedure for determining its PDCCH assignment. Aspects of the PDCCH assignment procedure and how UEs would monitor the control region to find PDCCH for them to obtain DCI were still in development at the Priority Date. The following paragraphs set out the basic parameters of the PDCCH as far as it had been specified in the relevant TSs at the Priority Date.
74. The format of the PDCCH is set out in Section 6.8.1 of TS 36.211 v.8.1.0 (the version current at the Priority Date):
6.8.1 PDCCH formats
The physical downlink control channel carries scheduling assignments and other control information. A physical control channel is transmitted on an aggregation of one or several control channel elements (CCEs), where a control channel element corresponds to a set of resource elements. Multiple PDCCHs can be transmitted in a subframe.
The PDCCH supports multiple formats as listed in Table 6.8.1-1.
Table 6.8.1-1: Supported PDCCH formats
|
PDCCH format |
Number of CCEs |
Number of PDCCH bits |
|
0 |
1 |
|
|
1 |
2 |
|
|
2 |
4 |
|
|
3 |
8 |
|
75. It had been determined that control channels would be formed by the aggregation of control channel elements (CCEs), where a CCE corresponds to a set of REs. When the eNodeB determines that messages need to occupy multiple CCEs, they are sent by the eNodeB using CCE aggregation. Aggregation of the CCEs had to be done in a structured way. It had been decided that the PDCCH message could be in one of four formats (0, 1, 2 and 3), corresponding to CCE aggregations of 1, 2, 4 and 8, respectively. An aggregation level of 4, for instance, means that four consecutive CCEs are combined. The number of REs that each CCE would comprise (and therefore the number of bits in the different PDCCH formats), and whether this would be determined according to the system bandwidth, had not been specified in the relevant TS at this stage.
76. It had also been decided that the PDCCH would occupy a region at the beginning of each subframe, referred to as the “control region”. It had been decided that the region in time occupied by the control region could be the first one, two or three symbols, which could be altered dynamically by a Control Format Indicator (CFI), which is sent on the Physical Control Format Indicator Channel (PCFICH).
77. The UE would be required to monitor a set of candidate control channels in the control region as often as each subframe (see section 9.1 of TS 36.213 v.8.1.0):
9.1 UE procedure for determining physical downlink control channel assignment
A UE is required to monitor a set of control channel candidates as often as every sub-frame. The number of candidate control channels in the set and configuration of each candidate is configured by the higher layer signaling.
A UE determines the control region size to monitor in each subframe based on PCFICH which indicates the number of OFDM symbols (l) in the control region (l=1,2,or 3) and PHICH symbol duration (M) received from the P-BCH where ![]() . For unicast subframes M=1 or 3 while for MBSFN subframes M=1 or 2.
. For unicast subframes M=1 or 3 while for MBSFN subframes M=1 or 2.
Other downlink physical channels in the control region
78. In addition to PDCCHs, some of the REs in the control region are used for other purposes. The UE can determine for each subframe which REs have been allocated by the eNodeB for the PDCCH. It does so based on system characteristics and on parameters broadcast by the network:
Transmitting Downlink Control Information (DCI) on PDCCH
80. Different DCI formats for sending different kinds of control information were created. At the Priority Date, several different DCI formats had been defined.
81. The format of the DCI messages sent on the PDCCH is determined in the eNodeB. The DCI format used affects the size of the DCI message, and hence the minimum number of CCEs required to transmit it. A DCI message may be short enough to fit in a single CCE. For longer DCI messages, more than one CCE is needed. DCI formats that are larger in size can be sent in a PDCCH format with a higher CCE aggregation (e.g., PDCCH format 2 which aggregates 4 CCEs in a PDCCH, or PDCCH format 3 which aggregates 8 CCEs in a PDCCH). The CCE aggregation level required also depends on the level of coding redundancy required to provide robust signaling to a UE. When the channel conditions to a given UE are poor, for instance, the eNodeB will include more error correction information, resulting in a longer message. (The terms “quality” or “geometry” are sometimes used to describe channel conditions.) A DCI message sent at a higher coding rate, providing greater redundancy, requires more CCEs for the PDCCH than the same DCI message sent at a lower coding rate.
UE ID
82. Each UE in a cell is given a specific Radio Network Temporary Identifier (RNTI) for identification of that UE in that cell (the C-RNTI). The network issues the RNTI. The C-RNTI is 16-bits long; and theoretically could be a number ranging from 1 to 65535. It was referred to in the evidence and many documents at trial just as the “UE ID”.
Search spaces and blind decoding of PDCCHs
83. Once the DCI message is generated and channel coded according to the required DCI and PDCCH format, it is mapped onto CCEs in the control region. A PDCCH that may carry control information for a UE is described as a “PDCCH candidate” for that UE. Once the UE has ascertained which CCEs are allocated to the PDCCH, it needs to analyze the PDCCH to determine whether its content is directed to that UE (known as “blind decoding”, also referred to below). Section 9.1 of TS 36.213 v.8.1.0 specified that each UE monitors a set of PDCCH candidates within the control region to find its own control information.
84. The RNTI is used to scramble the CRC of the PDCCH. This process is also called “masking” the CRC with the UE ID.
85. To detect whether a PDCCH contains control information for a UE, the UE searches for its ID in the masked CRC of the PDCCH. This is referred to as “blind decoding”.
86. The number of PDCCH candidates at each aggregation level, and the number of different DCI formats that each PDCCH aggregation level might carry, determines the maximum number of blind decoding attempts required by a UE in a search space. As there are several different downlink control formats, and four different PDCCH formats (aggregation levels), the number of PDCCH candidates monitored may be large. Attempting to decode the entire control region, applying all the possible PDCCH formats and DCI formats would be a substantial burden on the UE especially when the control region spans 3 symbols. To reduce this burden, a UE would only be required to attempt to decode a subset of all possible PDCCH candidates. This subset was called a search space.
Knowledge of hashing functions and random number generation
88. A hashing function is any function that can be used to map data of potentially arbitrary size to fixed sized values. In other words, it is a function that allocates a large number of inputs to a small known number of outputs.
90. The skilled person knew that computer languages such as MATLAB, C and C++ have pseudo-random number generators built into them and would have used such generators.
91. This is one of a number of areas of the CGK where there was some agreement (which I have just set out) but also areas of disagreement. I return to the disputed aspects below. From here on I refer to “random” numbers as generated by computers, even though in fact they are deterministic and actually pseudo-random, as explained above. This usage was adopted pretty consistently at trial.
Simulations
92. MATLAB was one software package used for running simulations. There was a minor disagreement about simulations, which I cover below.
Processor word size
Modulo operation
95. The skilled person would be familiar with the modulo operation. This was the limited extent of agreement about the CGK on modular arithmetic; I cover the disagreement below.
Technical Background - Collisions and Blocking
97. In the specific context of search spaces on the PDCCH, a “collision” refers to the search spaces completely overlapping (i.e., starting at the same location). To illustrate this concept, the example below shows, for the purpose of illustration, one way that the search space for several UEs might be arranged. The search space for each UE is shown in a different colour. In the diagram, the size of the search spaces at each aggregation level is 6 aggregations at each of aggregation levels 1 and 2, and 2 aggregations at each of levels 4 and 8.
98. For each subframe, the eNodeB chooses where within each UE’s search space to allocate DCI messages for that UE. One possible such choice is shown in the “eNodeB allocation” section of the diagram above. In this example, the eNodeB is sending one message for each UE. The eNodeB has chosen the aggregation level for each UE, and identified an arrangement for all the messages so that each UE’s message is within that UE’s search space at the appropriate aggregation level. This process is repeated in each subframe.
100. In other circumstances, search spaces can completely overlap - i.e. there is a collision - but there is no blocking. For instance, in the example in the previous paragraph, if the eNodeB only wanted to send messages at aggregation level 8, to two of the three UEs, it could do so.
101. Blocking may also arise because of the interaction between aggregation levels. In the diagram above, the eNodeB could send an aggregation level 8 message to each of UEs 1-4 but doing so blocks any messages to UEs 5 and 6.
102. If only two UEs are being considered and there are enough CCEs available, there will never be a situation where a message to one UE blocks a message being sent to the other. In practice, blocking arises because there are more than two UEs and/or there are too few CCEs. (This paragraph assumes that the search space at each aggregation level contains more than one CCE aggregation at that aggregation level.)
103. A collision is not the same as blocking. From a system viewpoint, it is blocking, not collisions, that is important. It would also not be correct to think of blocking as meaning that communication as a whole is prevented. In the example above, each of the three UEs can still receive a DCI message in two out of every three subframes. This is illustrated further in the figure below:
104. The figure shows three subframes with 32 CCEs for PDCCH in each, and illustrates the search spaces for three particular UEs at aggregation level 8. In this illustration, all other aggregation levels are omitted, and the CCEs forming part of the search space but not used for a DCI message are shown shaded. In this case, there is a persistent collision between the three UEs, meaning that each UE has the same search space in each of the three subframes (CCE#8 to 23, i.e., two aggregations at aggregation level 8). So the eNodeB cannot send a DCI message at aggregation level 8 to each of these UEs in each of these subframes. There is blocking; some communication is prevented. However, the eNodeB could still send DCI messages to each UE in two out of the three subframes, and the overall effect is therefore to degrade the connection between the eNodeB and each UE, without necessarily breaking it.
Disputed common general knowledge
105. I now turn to the areas where there was either a wholesale dispute about CGK, or where there was some agreement (set out above) and residual disagreement.
LCGs
106. The following information is not information that the skilled person would have at the outset of their consideration of Ericsson. It only comes in if they found a problem with the Ericsson function and looked to the literature in the way that Apple alleges. Since, for reasons that I explain below, I accept Apple’s submissions in that respect, the following information is relevant to obviousness though not CGK as such, and I set it out here for readability of the following sections of this judgment. I explain below when I deal with obviousness how the skilled person would get to the information and in particular to Knuth. I also deal there with the limitations of LCGs that the skilled person would become aware of in getting to Knuth, and from routine research generally. At this stage, I am just setting out the basics.
107. An LCG is a random number generator with the following form:
Xn+1 = (AXn + B) mod D
108. Various different letters are used in the evidence and exhibits for A, B and D. I am going to use A, B and D where possible because those are the letters used in the claims and in important parts of the evidence.
109. The form of LCG set out above shows how and why it is recursive. The LCG will generate a sequence of numbers in the following way (which I express in somewhat lay terms for present purposes):
i) You take the previous value in the sequence, which was Xn
ii) You multiply it by A. A is thus the multiplier.
iii) You add B. B is thus the increment.
iv) You take mod D of the result. D is the modulus.
v) The process is repeated.
110. The sequence has to start somewhere, and that is called the seed (or start value, or initial value, or similar).
111. Eventually the sequence will repeat. The number of iterations before repeating is called the period. The period cannot, for obvious reasons, exceed the modulus, but it may be less. Maximising the period depends on the parameters chosen. Poorer choices will lead to a shorter period.
Experience of RNGs/LCGs
112. This is perhaps more a point about the skilled person than CGK, but I will deal with it here because that is where Optis put it. The issue is over how much experience the skilled person would have of practically using random number generators (“RNGs”) within RAN1.
113. Prof Lozano gave a couple of examples of the use of RNGs in 3GPP. One was from RAN2 and left to implementation the specific RNG to be used. So it is not evidence in itself of any particular engineers in 3GPP using RNGs, but it provides some indirect evidence that it was expected that such engineers could conduct the necessary implementation.
114. The second example was of the use of an LCG, where the function appeared to have been taken (“stolen”) straight from a source called Numerical Recipes in C (“NRC”, which I discuss further below) without (Optis said) showing any assessment of the appropriateness of what was chosen. Optis argues that this shows that the skilled person could only perform uncomprehending lifting of RNGs/LCGs from the literature. I do not think it shows that that was all that they could do, just that that is all they did on that occasion. This conception of the skilled person as not understanding what they were doing is wrong in principle, in my view, and also inconsistent with the teaching in NRC and Knuth encouraging the reader to think and understand their choices, and with what the Patents expect of their reader.
115. So these examples do not help Optis. They provide some modest evidence of the actual use of RNGs/LCGs in the field. I accept that in RAN1 (or RAN2) the need to choose a random number generator arose relatively infrequently, but in itself that does not mean much.
116. In a similar vein, Optis argued that there were cases referred to in the documents such as NRC of skilled mathematicians botching LCG implementations. I accept that this would lead the skilled person to exercise care, which is what the law deems and requires to be used in any event, but I do not accept that it would deter the skilled person from using an LCG if it otherwise appeared suitable. Optis also said that the same considerations would lead the skilled address to stick to off the shelf solutions. I reject this for very similar reasons, but in any case it is clear that whatever the skilled person did, including with an off the shelf solution, they would have to check that they had made the right choice, and care would be needed then too. They would also want to think about whether the choice they made was overengineered for the application and hardware, and that too would require understanding.
117. All in all therefore I reject the argument that the skilled person would be someone who did not understand what they were doing with RNGs and/or thereby lacked confidence so that they only used off the shelf solutions.
Hashing functions v random number generators
118. This dispute was related to the dispute about self-contained v. recursive functions which I cover in connection with obviousness, below. Optis argued that it was CGK that hashing functions are necessarily self-contained while RNGs are necessarily recursive, and that for this and other reasons the two were regarded as quite separate and distinct concepts.
119. Indeed, Counsel for Optis began his closing submissions, Optis’ main oral argument in the case, by saying that “this is a case about hashing functions” and Apple wanted to “make this a case about random number generators”.
120. I think this was artificial; an attempt to create a conceptual difference that would not be seen by the skilled person to matter. My reasons include:
i) Counsel for Optis had opened the case by saying that “Hashing functions do involve randomisation as a means of achieving an even or uniform distribution, as your Lordship has obviously got”.
ii) The goal of a hashing function is to spread a large number of inputs evenly over a smaller number of outputs. The even spread may be achieved by mimicking a random spread.
iii) Ms Dwyer accepted that hashing functions that are uniform and random are good.
iv) The terms “hashing function” and “randomisation function” are used interchangeably in the art, including in the secondary evidence relied on by Optis, as Ms Dwyer also accepted. Ms Dwyer’s own written evidence in relation to Ericsson referred to the “randomization” and “randomness” of the hashing function.
v) Knuth’s chapter on hashing cross-refers to the chapter on random numbers. Optis sought to downplay this, but Ms Dwyer accepted that the direction was to look to the chapter on random numbers in connection with getting a hashing function whose overall output was random.
121. I therefore reject the argument that it was CGK (or would emerge from routine research) that hashing functions and random number generators were separate and distinct from one another.
Recursive v. self-contained
122. This was another point which bridged CGK and obviousness. It is convenient to deal with it here under CGK, as Optis did.
123. Optis argued that there was a fundamental difference between a recursive function (which an LCG is, because the production of each number uses the previous answer as an input as I have explained above) and a free-standing or “self-contained” function such as that in Ericsson, where the nth number in the sequence produced can be calculated directly without deriving the previous ones first.
124. Prof Lozano explained that it was possible to write a recursive function in self-contained form, and he showed how to do that for the LCG of the Patents’ claims. His approach assumed that C would be constant; although that it is true, I accept his evidence that it would be possible to provide a self-contained version for varying C.
125. However, the more basic point made by Ms Dwyer in response was that the self-contained form would require massive calculation that was not achievable in reality because it would involve raising A (which is for example 39827) to the power of 10 for the 10th subframe.
126. Prof Lozano retorted that it was not necessary to calculate 3982710 as such, because in modular arithmetic one could repeatedly multiply by 39827 and take mod D; the numbers would be kept much smaller.
127. In the last step of this debate in the written evidence, Ms Dwyer pointed out that Prof Lozano’s use of modular arithmetic just meant doing the recursion in question as part of the calculation of the purportedly self-contained form of the function. Following the oral evidence, I agree with her on this. So whether or not one actually calls it self-contained as a matter of semantics, Prof Lozano’s reformulation would still require the skilled person to use recursive methods of calculation.
128. For what it is worth, it is also possible to convert a self-contained function into a recursive form.
129. Although Ms Dwyer was therefore right, and there is a difference between self-contained and recursive functions, I did not think that there was any reason for the skilled person to care, or to be worried by using a recursive function, or to regard the difference as a radical or practically significant one. Working out the one millionth term of a recursive function might be computationally too intensive, but in the circumstances of the PDCCH all that would be needed would be to work out and store ten values for each aggregation level. That would not present any difficulty. Ms Dwyer ultimately accepted that there was no practical problem so as to put the skilled person off from using an LCG merely because it was recursive.
130. For what it is worth, the secondary evidence supports that view (two queries about the function being recursive were made but well met by LGE’s explanation that few iterations were needed), but I think it would be apparent anyway.
Simulations
131. I was unclear what dispute remained over this by the end of the trial. I find that it was CGK to use simulations with tools such as C, C++ or MATLAB to test proposals that were made during RAN1 work. The simulations were done at the meetings and outside meetings.
132. It is possible that there was some dispute about whether laptops of the priority date were powerful enough for all such simulations. I find that even if and to the extent they were not, it was CGK to use more powerful computers available as part of the “back room” support to RAN1 delegates.
Modular arithmetic
133. The experts agreed that some aspects of modular arithmetic would be CGK, in particular, as noted above, the “mod operation”. That is no more than the exercise of finding a remainder, so 17 mod 3 = 2, or 1000 mod 111 = 1.
134. However, the experts disagreed about whether the “distributive property” of modular arithmetic would be CGK.
135. The distributive property was explained by Prof Lozano as:
(X+Y) mod C = (X mod C + Y mod C) mod C.
136. This is not complicated. In the left hand side of the equation you add X and Y and take the remainder after dividing by C. In the right hand side of the equation you divide by C and take the remainder for X and Y separately and then add the remainders. But that might be greater than C, so you perform the mod C operation on the total. In each case you are just getting rid of all the multiples of C.
137. It is artificial to say that the mod operation would be CGK but this would not, and I accept Prof Lozano’s evidence that the distributive property would also be CGK.
138. Ms Dwyer also said that the skilled person could perform modular arithmetic to the level of plugging numbers into equations but could not work with modular relationships expressed in variables. I reject this too, as artificially hobbling the skilled person, and because it is inconsistent with what the Patents envisage they could do, and I again prefer Prof Lozano’s view. I thought there was also a tension between Ms Dwyer’s conception of the skilled person being limited in this way and her positive suggestions about what might be done from Ericsson, such as changing x, which I felt would require a degree of understanding of modular arithmetic in excess of what she envisaged.
139. Optis’ motive in denying that this particular bit of modular arithmetic - the distributive property - was CGK is that it is the tool needed to appreciate that the Ericsson function would not work properly over successive subframes. Optis sought to use the fact that (it says) some of the RAN1 participants did not spot that problem to argue that the skilled person would not have the characteristics as I have just indicated. I reject this. Of course it is not necessarily the case that the skilled person who had those characteristics would use them without hindsight to spot the problem with the Ericsson function, but that is a question in relation to obviousness rather than CGK.
Max hits
140. A metric that is used in the simulations presented in the Patents is maximum number of hits or “max hits”. Optis contended that it was not CGK.
141. I think Optis is right about that. Performing simulations was CGK, and it would be down to the skilled person performing simulations for a given purpose to choose appropriate metrics to assess the degree of success or failure of the function or system under test. The skilled person would not know as a matter of CGK that max hits was a metric to use. That does not mean that it was a good metric, or that they could not work out that they should use it in a given situation, but that is something that comes in at the obviousness stage of the analysis.
The Patent
142. The specification begins with some general teaching about LTE and the PDCCH, at [0004] to [0006]. Thereafter, it identifies Ericsson at [0007]. The specification then goes at length into the meaning and use of the function of claim 1 that I explain below. It involves the use of an LCG and a “mod C” operation.
143. From [0096] onwards, the specification starts to describe the choice of parameters for the LCG. It explains at [0099] that it will use the concept of number of “hits” (which essentially means collisions) as a criterion. At [0103] it explains that it will be looking at average number of hits and maximum number of hits, as well as whether the range 0 to C-1 is uniformly covered by the start positions generated, and the variance of probabilities that values between 0 and C-1 will be generated (another measure of uniformity).
144. Tables 2, 3 and 4 are then presented, giving values for those metrics for various combinations of the parameters A, B, C and D.
145. [0107] and [0108] give some guidance as to the choice of parameter D, which is the modulus. It refers to the size of D and to whether D is prime. At [0109] it recommends choosing D = 65537 when the UEID is a 16-bit number.
146. In written evidence which was essentially unchallenged, Prof Lozano said that [0107] and [0108] were unreliable, or at least very badly written, because (paraphrasing for simplicity) they misunderstand or mis-explain the importance of the size of D on the one hand, and whether it is prime on the other. I accept that evidence. [0107] and [0108] are not very clear or useful. They certainly give less good guidance about the choice of D than would be provided by Knuth (I make this observation since it is of potential relevance to Apple’s insufficiency squeezes).
147. [0112] recommends that B is set to zero. In that preferred situation, the LCG will be a multiplicative LCG (as to which, see below).
148. Prof Lozano also gave evidence that Tables 3 and 4 (in particular the latter) contain errors. A particular problem is that they do not specify C, with the result that they cannot be replicated. Prof Lozano attempted to work out what had been done, and did manage to verify that the max hits column in Table 4 would make sense if C were 16. But that would mean the other columns were wrong. I return to this in relation to the insufficiency allegations.
Claims of the Patent in issue
149. As I have already said, it was agreed the issues can be dealt with by consideration of claims 1 and 4 of the Patent, which are as follows (taken from Apple’s written opening submissions where reference letters for the claim features were added, though nothing turns on them).
150. Claim 1:
1[a] A method for a User Equipment, UE, to receive control information through a Physical Downlink Control Channel, PDCCH, the method comprising:
1[b] receiving control information from a base station through the PDCCH in units of Control Channel Element, CCE, aggregations, each of the CCE aggregations including at least one CCE in a control region of subframe 'i'; and
1[c] decoding the received control information in units of search space at subframe 'i',
1[d] characterized in that the search space at subframe 'i' starts from a position given based on a variable xi and a modulo 'C' operation, wherein 'C' is a variable given by: C = floor(NCCE /LCCE),
and wherein 'xi' is given by: xi = (A*xi-1 + B) mod D,
wherein A, B and D are predetermined constants, and x-1 is initialized as an identifier of the UE, and NCCE represents the total number of CCEs at subframe 'i', and LCCE is the number of CCEs included in the CCE aggregation, and floor(x) is a largest integer that is equal to or less than x.
151. Claim 4:
4[a] The method according to claim 1 or 2,
4[b] wherein D, A, and B are 65537, 39827, and 0, respectively.
152. Claim 1 was used as an exemplar of an “unspecified” claim, which refers to the fact that A, B and D are not assigned specific values. Others of the Patents also include unspecified claims, and it was agreed that my decision on claim 1 would determine those claims as well.
153. Claim 4 was used as an exemplar of a “specified” claim, since D, A and B are set. Again, it was agreed that my decision on claim 4 would allow determination of all the unspecified claims in all of the Patents.
154. As Optis pointed out, claim 1 of the Patent uses the notation xi, while the text of the specification refers to Yk. It does not make any substantive difference, but it needs to be borne in mind for one’s understanding. The “i” or “k” denotes the subframe number.
155. The claims do not make it easy to see what is going on, or to capture the inventive concept. Essentially, however, what claim 1 is saying is that for each subframe, the start position of a PDCCH search space is found using an LCG, with the output of the LCG being subjected to a modulo C operation.
156. For the initial “seed” value for the LCG, the UEID is used. For subsequent subframes the LCG works recursively, as explained above.
157. C is the number of possible start positions, and is found by taking the number of CCEs in the subframe and dividing by the aggregation level L (if CCE is not precisely divisible by L then the “floor” operation takes only the integer part). So if there are e.g. 64 CCEs and the aggregation level is 8, then there are 8 possible starting positions. Taking mod C will give a number from 0 to C-1.
158. It is incorrect to say, as Apple sometimes did, that claim 1 is just to the use of an LCG to find the start positions of the search space. The LCG is, as Ms Dwyer put it, “nested” with the mod C function. It is important not to lose sight of this, since one of Optis’ obviousness arguments relies on it.
The Prior Art
159. I will now set out the disclosure of Ericsson, and then of Knuth. They do not cross-refer to each other, and so it is only legitimate to read them together if they are shown to be CGK or if routine research from one would lead by obvious steps to the other.
Disclosure of Ericsson
160. Ericsson is a 7-page slide presentation.
161. Page 1 set out the “Agreement so far” and is fairly self-explanatory once one understands the CGK:

162. Page 2 explains about the search space (it was not yet finally agreed that CCEs in a set would be contiguous but that does not matter to the arguments):

163. Page 5 gives some details of the UE-specific search space, which is the territory of this dispute:

164. Down to this point there is little if any disagreement between the parties. Page 6 is the key page over which the obviousness dispute takes place:

Disclosure of Knuth
165. It is not practical to reproduce all the parts of Knuth relied on. I will summarise its main contents.
166. Apple relies on 40 pages from Chapter 3 of volume 2. Chapter 3 is entitled “Random Numbers”. Optis relies on other pages from that chapter and on the part of volume 3 (“Sorting and Searching”) which concerns hashing functions. In my view it would not be open to Apple to restrict the way in which the skilled person would view Knuth by artificially limiting consideration to selected pages, but I do not think it attempted to do that. It would have been impractical for it to cite the whole book, and no doubt if it had done so Optis would, rightly, have objected. Consideration of the 40 pages cited ought to take place in the context of the rest of the work that the skilled person, guided by CGK, would have considered relevant.
167. After a general introduction there follows section 3.2 “Generating Uniform Random Numbers”. The first method introduced is the class of LCGs, which are described as “[b]y far the most popular random number generators in use today”. After setting out the form of the LCG, Knuth observes that choosing the “magic numbers”, meaning A, B and D, appropriately will be covered later in the chapter. It explains that sequences from LCGs have a period and that “A useful sequence will have a relatively long period.”
168. At the top of page 10, Knuth says that “The special case c = 0 deserves explicit mention”. He uses c to denote the increment, so in terms of the A, B and D letters I am seeking to use, he is referring to B. He identifies that this case is referred to as “multiplicative”, and says that it is quicker but tends to reduce the period.
169. Thereafter, Knuth gives advice on the choice of modulus, which he says at 3.2.1.1 should be “rather large” and notes that its choice affects speed of generation. He deals with choosing a modulus when the word size of the computer in question is w (the word size is 2e for an e-bit binary processor) and discusses the case where the modulus is set to w+1 or w-1, providing Table 1 which gives the prime factorisations for various values of e. I will return to this below, in particular in relation to the specified claims.
170. Choice of multiplier is discussed from 3.2.1.2. Knuth explains that its intention is to show how to choose the multiplier to give maximum period, and that “we would hope that the period contains considerably more numbers than will ever be used in a single application”.
171. Further specific advice is given for particular cases over the following pages. For example, getting a long period with an increment of zero (the multiplicative case) is covered at page 19, and says that with an increment of zero an effectively maximum period can be achieved if the modulus is prime.
172. Some of the analysis and proofs are unquestionably complex, but I think Ms Dwyer overstated it when she called them “impenetrable”. It may well be that the skilled person would not feel the need to follow through the proofs, though.
173. Section 3.2.2 on page 25 introduces “Other Methods”, i.e. other than LCGs. This contains the caveat that a common fallacy is to think that a small modification to a “good” generator can make it even more random, when in fact it makes it much worse.
174. Section 3.3 from page 38 then introduces statistical tests to test if sequences produced are in fact random.
175. As I have said, Optis relied on other parts of Knuth. I deal below with its reliance on the part of volume 3 concerning hashing functions. The other material added, via Ms Dwyer’s evidence in her reply report (her fourth, her having put in two reports for Trial B), was the remainder of chapter 3.
176. When Ms Dwyer introduced the rest of the chapter she did so for the limited purpose of highlighting section 3.4.1 on generating small random numbers. But the main purpose for which the rest of the chapter was used at trial by Optis was to highlight the summary at section 3.6 from page 170, to which Ms Dwyer had not drawn attention. This gave recommendations for “a simple virtuous generator” and gave advice for the choice of the modulus, multiplier and increment. Optis’ position was that that was what the skilled person would use if they maintained an interest in LCGs. It recommends a modulus of at least 230.
Obviousness
177. I will deal with the legal principles first.
Legal principles
178. At one level there was no dispute about the basic principles. As in other recent decisions I was referred to Actavis v. ICOS [2019] UKSC at [52] - [73], with its endorsement at [62] of the statement of Kitchin J as he then was in Generics v. Lundbeck [2007] EWHC 1040 (Pat) at [72].
Existence of alternatives
179. Apple relied on Brugger v. Medicaid [1996] RPC 635 at 661, approved by the Supreme Court in Actavis v. ICOS, to the effect that an obvious route is not made less obvious by the existence of other obvious routes. This principle is of course often relied on by those attacking patents for obviousness, and it is valid as far as it goes, but it must not be overdone. Optis referred to Evalve v. Edwards [2020] EWHC 514 (Pat) at [256] - [258] where Birss J pointed out that what Brugger said is that the existence of alternatives does not itself rule out obviousness, but also that their existence may be one relevant factor, as Actavis v ICOS and Generics v Lundbeck spell out.
Secondary evidence
180. Optis relied to an unusually heavy degree on evidence of what others in the field - RAN1 participants - said or did, either pre-priority or post-priority in reaction to the alleged invention of the Patents.
181. Optis relied on this for two purposes, which I think were not entirely distinct.
182. The first was in connection with identifying the notional skilled person and their abilities and knowledge. This is certainly legitimate - see e.g. Unwired Planet v. Huawei [2017] EWCA Civ 266 at [113]-[114] where Floyd LJ said that it would be unreal for an expert not to seek to understand the 3GPP context. Indeed he said that an expert who did not try to understand the context would be falling short in their duties. Both sides used the historical RAN1 context in this broad sense, although Ms Dwyer gave much more attention to it.
183. The second was to contend that in particular respects RAN1 participants behaved in specific ways, and that it could be inferred that that is how the notional skilled person would behave. Optis contended that only a subset of RAN1 participants spotted problems with Ericsson and that despite coming up with proposed ways forward, none of them apart from LGE thought of the solution of the Patents.
184. This use of secondary evidence requires caution, as the authorities indicate. Laddie J in Pfizer’s Patent [2001] FSR 16 at [63] said the following in the relation to secondary evidence when there is more than one route to a desired goal:
“63. Of particular importance in this case, in view of the way that the issue has been developed by the parties, is the difference between the plodding unerring perceptiveness of all things obvious to the notional skilled man and the personal characteristics of real workers in the field. As noted above, the notional skilled man never misses the obvious nor sees the inventive. In this respect he is quite unlike most real people. The difference has a direct impact on the assessment of the evidence put before the court. If a genius in a field misses a particular development over a piece of prior art, it could be because he missed the obvious, as clever people sometimes do, or because it was inventive. Similarly credible evidence from him that he saw or would have seen the development may be attributable to the fact that it is obvious or that it was inventive and he is clever enough to have seen it. So evidence from him does not prove that the development is obvious or not. It may be valuable in that it will help the court to understand the technology and how it could or might lead to the development. Similarly evidence from an uninspiring worker in the field that he did think of a particular development does not prove obviousness either. He may just have had a rare moment of perceptiveness. This difference between the legal creation and the real worker in the field is particularly marked where there is more than one route to a desired goal. The hypothetical worker will see them all. A particular real individual at the time might not. Furthermore, a real worker in the field might, as a result of personal training, experience or taste, favour one route more than another. Furthermore, evidence from people in the art as to what they would or would not have done or thought if a particular piece of prior art had, contrary to the fact, been drawn to their attention at the priority date is, necessarily, more suspect. Caution must also be exercised where the evidence is being given by a worker who was not in the relevant field at the priority date but has tried to imagine what his reaction would have been had he been so.”
185. And there are many general statements in the authorities stressing that secondary evidence is, indeed, secondary. E.g. Molnlycke v Procter & Gamble [1994] RPC 49 at 112:
“Secondary evidence of this type has its place and the importance, or weight, to be attached to it will vary from case to case. However, such evidence must be kept firmly in its place. It must not be permitted, by reason of its volume and complexity, to obscure the fact that it is no more than an aid in assessing the primary evidence.”
186. Not infrequently, secondary evidence may be rejected simply because the workers in the field in question were not aware of the cited prior art (or it is unknown if they were aware of it). That does not apply here. The RAN1 workers in question were specifically aware of Ericsson and were working on it. So subject to the other caveats identified above, this is a case where the secondary evidence could be more likely than usual to play a role.
187. Another factor clearly established in the case law in relation to “why was it not done before” is the closeness in time between the prior art and the making of the invention. As Jacob LJ commented in Schlumberger v EMGS [2010] RPC 33 at [77]:
“[Secondary evidence] generally only comes into play when one is considering the question ‘if it was obvious, why was it not done before?’ That question itself can have many answers showing it was nothing to do with the invention, for instance that the prior art said to make the invention obvious was only published shortly before the date of the patent, or that the practical implementation of the patent required other technical developments.”
Prejudice/lion in the path
188. Apple characterised part of Optis’ case as being a “lion in the path” that was actually a “paper tiger”. What it meant was that Optis was relying on a perception that LCGs were flawed to the point of being useless. Apple said that Optis could not rely on such a perception unless the Patents overcame the prejudice by showing that LCGs were in fact valid for the purposes taught.
189. Apple relied on the well-known statement about prejudice by Jacob LJ in Pozzoli v BDMO [2007] EWCA Civ 588 at [28]:
“28. Where, however, the patentee merely patents an old idea thought not to work or to be practical and does not explain how or why, contrary to the prejudice, that it does work or is practical, things are different. Then his patent contributes nothing to human knowledge. The lion remains at least apparent (it may even be real) and the patent cannot be justified.”
190. Optis responded by citing the decision of Mann J in Buhler v. Spomax [2008] EWHC 823 (Ch). Mann J cited the above passage in Pozzoli, and also referred to what Jacob LJ had said when a judge at first instance in Union Carbide v. BP [1998] RPC 1, that invention can lie in “finding out that that which those in the art thought out not to be done, ought to be done.” Mann J went on to say that those dicta did not require in all cases that a patent must explain why the prejudice is wrong and how it works, in scientific language.
191. I do not think there is anything incompatible between the views of Jacob LJ and Mann J. In the right case it might be possible really and usefully to dispel a prejudice by a single experiment showing a positive result without a scientific explanation. It will depend on the facts. Often, though, a single unexplained result will not allow a general conclusion to be drawn, in which case the prejudice will not have been dispelled at all, or not enough to justify a broad claim. I do not need to go into this any more deeply because for reasons I explain below, I do not think there was a prejudice against LCGs in the normal sense that “prejudice” is meant in patent law. Rather, there was a perception that they had some severe potential limitations but could be all right for undemanding applications.
Technograph and number of steps
192. Optis emphasised the very well-known Technograph principle that salami-slicing the gap between the prior art and the patent into small steps and then putting forward reasons for each one is prone to inject hindsight. I accept this, of course.
193. In furtherance of arguing that Apple’s case suffered from this vice, Optis produced a document in closing which purported to split Apple’s argument into 19 steps starting from Ericsson (the document showed 17, but step 2(5) had three sub-steps) and 18 somewhat different steps from Knuth.
194. For its part, Apple argued that its case involved only three steps, at least to the unspecified claims.
195. I do not think there is any particular way in which steps along an obviousness argument must be split, or counted. The patentee has an incentive to maximise them and the defendant to minimise them. Sometimes steps are genuinely independent and sometimes they are closely related. Some steps are much more important than others (e.g. Counsel for Optis agreed that Optis’ step 2(2) was “not a massive point”, which was a euphemism for “trivial”). Some steps do not arise at all if some other proposition goes against a party, and so for example Optis’ step 1(1) was to identify the problem of “lockstep” collisions in Ericsson, whereas Apple’s argument was that that was unnecessary because the skilled person would do simulations anyway.
196. What is however important overall is for the Court to be sensitive to whether the gap between prior art and patent is being deconstructed in such a way as to build in hindsight, and I have borne that in mind in this case.
“Could/would”
197. Optis submitted that it is not enough for a finding of obviousness that the skilled person could do something, but that it must rather be shown what they would. This “could/would” distinction is often referred to in the case law of the EPO. It is not an absolutely inflexible rule and must be taken into consideration along with the principles that apply where there are multiple obvious options, or where a parameter in a claim is arbitrary. I will bear it in mind, but the reason Optis stressed it was because it wanted to limit the effect of oral evidence that Ms Dwyer gave phrased in terms of “could”. I deal with this below.
Pozzoli
198. Neither side used the structured Pozzoli analysis. I could not see why not, although I do not think it was critical to do so in this case.
Obviousness over Ericsson
199. I now turn to assess the argument of obviousness over Ericsson. Although the parties did not express their submissions in terms of Pozzoli, I find the structure useful.
Pozzoli questions 1 and 2
200. I have addressed the skilled person and the CGK above. I am proceeding on the basis of the RAN1 skilled person.
Pozzoli question 3
201. The difference between Ericsson and the unspecified claims of the Patents is the use of the function of those claims instead of the Ericsson function.
202. Apple sought to minimise the difference (though not phrasing it in terms of Pozzoli) by emphasising that the mod C operation is common to both, and characterising the step as replacing only K*x + L in Ericsson with the LCG of the Patent claims.
203. I reject this as an unfair approach because it implicitly assumes that the skilled person would see the Ericsson function as being in two parts with the first replaceable on its own. For reasons given below I think the skilled person would see that, but it is a step on the obviousness argument and cannot just be assumed away at this stage of the analysis.
204. To put it another way, I agree with Optis that the inventive concept of the unspecified claims lies in the whole of the function and not just in the LCG part.
205. The inventive concept of the specified claims and the further gap from Ericsson that they represent, is the combination of values A=39827, B=0, and D=65537.
Pozzoli question 4 - unspecified claims
206. Apple’s case was that the skilled person would:
i) Verify whether the Ericsson function would provide “the desired properties” and conclude that it would not.
ii) Observe that the problem lay with the randomisation part of the Ericsson function (and not the mod C part).
iii) Do a literature search to find another appropriate hashing/randomisation function.
iv) Identify, ultimately from Knuth, LCGs as a good choice.
207. Optis split this process down into many more steps, as I have already said. I do not intend to go through them one at a time, but I have borne them in mind. Some of them were phrased in terms of not doing something (e.g. using Knuth’s off-the-shelf generator) and I thought those were misguided efforts to elevate the existence of alternatives into positive decisions that had to be made.
Assessment of the Ericsson function
208. The first point to note here is that the Ericsson document itself invites the reader to assess the function proposed, in the last bullet point “Verify that we get the desired properties by the above function”. Similarly, though less explicitly, thought is invited to ensuring that K and L, numbers different for each aggregation level and given by the specification, are “big enough”.
209. This means that the skilled person would assess whether the function worked, with the size of K and L in mind, among other things. I do not believe that Optis disputed that the skilled person would do this, or argued that the decision to make an assessment would be inventive. Such an argument would be hopeless anyway, since the document effectively directs an assessment.
210. The desired properties would be identified by the skilled person as being distribution of the starting positions of the search spaces randomly and evenly across the possible starting positions, over the subframes. There was no dispute between the experts that random and even distribution would be relevant properties, but there was a disagreement between them, which I thought was really a semantic one, about how the start positions for successive subframes were to be considered. Thus Ms Dwyer did not accept that the desired properties included random and even distribution “across subframes”, but what she meant was that each single use of the function only gives the start position for one subframe (the subframe number being an input to x). This was related to the recursive/self-contained issue.
211. What the assessment would be and what it would yield was disputed.
212. Prof Lozano’s evidence was that the skilled person would realise that the function would not work. There were three strands to this:
i) An appreciation from an analytical common-sense check (or “eyeballing”) that the function would not work because if two UEs collided in one subframe they would collide in every following subframe. This is because for each UE x would be incremented by the same amount in each subframe. This problem arises because of the distributive property of modular arithmetic, which I have held to be CGK, in agreement with Prof Lozano and contrary to what Ms Dwyer said.
ii) An appreciation from similar “eyeballing” that the function would not work for C = 16.
iii) Performing simulations. Prof Lozano said that if the problem were not apparent from the analytical common-sense check then it would show up in simulations.
213. Ms Dwyer accepted that the skilled person might start by “eyeballing”. She accepted the reasoning that would lead to the conclusions that collisions would repeat and that C=16 would not work, and then there was this interchange (T3/401):
“Q. And they would see the same things that we have just discussed, so they would see the problem of the continuing collisions between subframes and they would see the problem of C=16 if they put some numbers in?
A. Certainly the C=16 I would suggest they would. The other one you would have to get the right UEIDs to find that to work, but yes.
Q. So whether the skilled person just eyeballs the Ericsson function, if I can put it like that, or whether they put some numbers in, then they are going to see that the Ericsson function does not have the desired properties?
A. Ultimately, probably they will come to that conclusion, yes.”
214. Optis sought to meet this in two main ways. First, it said that the secondary evidence showed that the “lockstep” problem (see below) was not an obvious one, and second it said that Ms Dwyer’s cross-examination as referred to above was about “could” and not “would”. I can deal with the second part first and briefly: passages shortly before the one quoted above did refer to “could”, but the passage quoted is squarely about “would” and that was my overall sense at the time.
215. On the first point, it is necessary to explain that Optis drew a distinction between “static” collisions and “lockstep” collisions. The former occur, it said, where the search spaces of two UEs collide in one subframe, and then in the same way in the next subframe, and the next subframe and so on. Optis did not say that appreciating this was inventive, or that the idea of reconfiguring from one subframe to the next to avoid it required insight. The latter, lockstep, was said to arise when UEs collide in successive subframes because despite reconfiguration each subframe their search spaces move around the possible options in the same way as each other, hence moving “in lockstep”. I agree that no one had articulated this concept in those terms, but that does not mean that noticing the first strand of the problems with Ericsson required insight. In any event, Prof Lozano rejected the distinction as not being of practical relevance, and Ms Dwyer did not make anything of lockstep in her written evidence, mentioning it occasionally in her oral evidence. Her acceptance that the lockstep problem would be noticed by the skilled person was more equivocal than for C=16 but taking the expert evidence as a whole and allowing for the risk of hindsight I readily conclude that it would be.
216. As to the secondary evidence, it is not very helpful and certainly nowhere near enough to displace the above clear consistency in the primary evidence that the Ericsson function would be identified by the skilled person as being deficient. Some of those that commented noticed the C=16 problem; Qualcomm and LGE noticed the lockstep problem (albeit of course that LGE’s input was from the inventor). NTT drew a diagram for C=16 but somehow did not spot that problem and I conclude based on Prof Lozano’s evidence that they made a mistake that the ordinary skilled person would not have. Likewise Prof Lozano said Nokia’s submission was wrong (in a different respect).
217. The picture is just far too patchy and inconsistent to draw any conclusion from these real people’s experience as to how the notional addressee would have behaved. Not only were the workers operating under pressure of time with, no doubt, other tasks to perform, but they also had their own interests to serve, for example with Qualcomm advocating “Gold” codes in which the company had a proprietary position.
218. A particular point that Optis ran on the secondary evidence was that the people who devised the Ericsson function must have known what they were doing, so it could be concluded that the lockstep problem must have passed them by (and therefore would not be spotted by the skilled person either). No doubt they were experienced and skilful and working hard on the problem, but the thinking behind the x=UE_ID*16 + subframe_number and (K*x+L) components of the scheme is not explained other than the aspiration that large values for K and L would be promising, and the function does not correspond to any particular known hashing function; perhaps they jumped to a conclusion that they should not have and perhaps they were optimistic but uncertain and were relying on the RAN1 community to spot any problems. That plus the explicit encouragement to “verify” prevents any argument that the skilled person would just accept that the function must be all right. The “verify” statement has the ring to it that the proposal is a provisional one and (so far as it is a matter for expert evidence) Ms Dwyer agreed that it bears the connotation that the function might not give the desired properties.
219. Optis’ best point on the assessment of the Ericsson function is that without knowing of the lockstep problem one would not look for it, and that although it is easy to appreciate its impact once explained, that is just symptomatic of hindsight. I have, as I said, borne this very much in mind, but based on the expert evidence I do not accept it. In any case, Prof Lozano’s evidence, which was not directly challenged (only via the secondary evidence, as it related to Motorola), was that if the problem was not identified analytically it would be found when simulations were done.
220. Overall I conclude that it is clear that the skilled person would conclude without the need for any insight that the Ericsson function was deficient as outlined above.
What to do next
221. Apple contended next that having realised that the Ericsson function was deficient, the skilled person would also realise something had to be changed. Ms Dwyer accepted that, and it is self-evident. It is not really a step at all.
222. What follows in Apple’s case does involve real steps. Apple’s position was that the skilled person would realise that the mod C part of the Ericsson function was there to “squeeze” the random output of the (K*x + L) part down from a large number to a range from 0 to C-1, that the mod C part was therefore necessary and was working all right, and that any change should therefore be to the random, (K*x + L) part.
223. Prof Lozano strongly supported this approach. For example, in cross-examination he said this:
“So, my Lord, a hashing function has two purposes. One is to map a big number of inputs down to a smaller number of outputs, so there is a squeezing process, and the other one is to randomise these mappings so that two very similar inputs do not get mapped to two very similar outputs to minimise confusions. So the mod C, the outer mod C, is doing the squeezing down part of the hashing, and it is a standard way of doing it. It has been used in 3GPP before. It had been proposed already many months before the priority date to do this squeezing down by Motorola, and it is actually in Ms. Dwyer's report. So that is well understood, the squeezing down. The discussion here, and the work that was taking place, was around the randomisation part, the randomisation part. So the randomisation part here is K x+L, right, because the rest is the mod C which is doing the squeezing down, concentrating the many input into the few outputs. So randomisation is done by K x+L and is not doing a good job at that.”
224. Later, he said:
“Well, like I said, the Skilled Person here is looking for something that randomises properly; that is it. That is all that is missing here. The rest is fine. The outputs are 0 to C-1 as they should be, so that part is functioning well. What is not functioning well is the randomisation part, so one would look to randomise things so you look at the book and see what it says about the number generators and pick an off-the-shelf solution.”
225. I accept this and think that while the skilled person would certainly have to think about the overall effect of the whole function, it would stand out clearly that the mod C part had the object and effect for which Apple contends. It would not require insight to retain mod C if possible (there is a specific point about using mod C which interfaces with the issues on the specified claims and with which I deal below).
226. Ms Dwyer came close to accepting much of this. She accepted that mod C would be seen as having the “squeezing down” effect to which I have referred. She said “I think people would look to change part of the equation, agreed, and the mod C does map the output to the range that is desired. So I think that if they were trying to keep it similar to the original format that is true.”
227. I therefore accept Apple’s contention that an obvious route was to retain mod C, on the basis that it was adequately performing a well-understood and necessary task, and look to remedy the problem, apparent at this stage, with the Kx + L randomisation part.
Literature search
228. With work focusing on changing (K*x + L), Apple’s case was that the skilled person would look in the literature for an appropriate RNG, and find LCGs in Knuth or other sources.
229. Ms Dwyer resisted strongly the proposition that the skilled person would look online or in a textbook for a RNG to replace (K*x + L). She said that was a leap and another simpler approach would be just to change x, which she said some of the RAN1 participants had looked at. Against that background she was asked whether it would be a reasonable or sensible route for the skilled person to look up an RNG. She replied that they could take that route.
230. Unsurprisingly, Counsel for Optis submitted that “could” was not good enough. I agree that in itself it is not, but my task is to weigh the evidence of Prof Lozano who clearly said that is what the skilled person would do (there being other possibilities, of course, and I have to weigh that up as well), against the evidence of Ms Dwyer who would not go that far, although my sense at the time was that she was as close as may be to accepting “would”.
231. I prefer Prof Lozano’s evidence; I found him the more persuasive expert for reasons given in my overall assessment of the witnesses above. One sensible thing to do would be to look in the literature for an established and understood way to generate randomness. I think it would be the most natural way forward, and certainly one of the leading ones. It is the reliable, routine, systematic approach of the uninventive skilled person.
232. Prof Lozano was fair in putting this forward. He did not reject other options as being possible. Ms Dwyer’s idea of modifying x was not really explored with him, but he was asked about the possibility of varying K and/or L by subframe, the idea put to him being that it would create more decorrelation between subframes. Prof Lozano agreed that changing K and/or L this way was something that the skilled person might do, and indeed it was discussed in RAN1 (suggested by Dr Parkvall).
233. I do not think the existence of such other options makes it any less natural or obvious that the uninventive skilled person would look for an established RNG. The Ericsson function had turned out to be bad for the task in hand; it was not of an existing type that was well-understood; the ideas of varying x or K and/or L were fine as concepts but the skilled person would not have had guidance from the CGK as to how to do it, so it seems a good deal less likely to appeal than looking to standard literature.
Getting to Knuth
234. Apple’s key point was that by one means or another, having embarked on a literature search, the skilled person would find their way to Knuth.
235. I accept this. Knuth is a standard reference work, a “bible”, and it is possible that the skilled person might get to it just by asking a librarian or similar. Apple’s case, though, was built on the skilled person taking either Wikipedia as a jumping-off point, or using NRC and getting to Knuth that way.
236. Prof Lozano specifically said that he thought NRC would be the most natural thing to turn to first, and since he himself had it on his shelves, that is what he did. I accept that that is what he did, and that it is representative of what the skilled person might well do.
237. However, there is a significant complication, which is that Prof Lozano had the second edition of NRC on his shelves, and there was a third edition, which he did not have, and which was published six months before the priority date. The difference is of great significance potentially, because the third edition strongly deprecates LCGs in ways which the second edition did not. I address this below.
238. No criticism is made of Prof Lozano personally for finding only the second edition of NRC (whereafter he was led to check out Knuth from his University library), but the legal issue for me is what was CGK to the notional skilled person. I have no doubt that the CGK will usually include the latest edition of established standard works, except perhaps in marginal cases where the latest edition is published very shortly before the priority date. That is not the case here. Apple’s case was that NRC was a CGK source, and it must live with the consequences that that must include the third edition, warts and all. Apple argued that the second edition did not stop being CGK. I do not accept that and it seems an impractical and unreal route to start down for patent cases generally, but it makes little or no difference because what the third edition makes clear is that the attitude of the art to LCGs was worsening over time. From here on where I refer to NRC I mean the third edition.
239. For these reasons, I think the CGK attitude to LCGs must be assessed from NRC, Knuth and, to a significantly lesser extent, Wikipedia. I accept Ms Dwyer’s evidence that the skilled person would not use Wikipedia as a sole source of specific functions, formulae or analysis, but she accepted that it was a useful starting point for finding something reliable, and there is a clear pointer to Knuth in it.
240. The third edition of NRC came into the case late; Counsel for Optis told me, and I accept, that it was only found shortly before trial because Optis had no reason to think Prof Lozano would not have used the latest edition. Accordingly, neither he nor Ms Dwyer put in written evidence on it specifically.
241. NRC Chapter 7 deals with random numbers. The last paragraph on page 340 and the first paragraph on page 341 say:
“The pragmatic point of view is thus that randomness is in the eye of the beholder (or programmer). What is random enough for one application may not be random enough for another. Still, one is not entirely adrift in a sea of incommensurable applications programs: There is an accepted list of statistical tests, some sensible and some merely enshrined by history, that on the whole do a very good job of ferreting out any nonrandomness that is likely to be detected by an applications program (in this case, yours). Good random number generators ought to pass all of these tests or at least the user had better be aware of any that they fail, so that he or she will be able to judge whether they are relevant to the case at hand.
For references on this subject, the one to turn to first is Knuth. Be cautious. about any source earlier than about 1995, since the field progressed enormously in. the following decade.”
242. This illustrates an important facet of Apple’s argument, which is that the skilled person would make a case-specific decision about how much randomness was needed. There is also a clear signpost to Knuth.
243. Section 7.1 of the same chapter includes the following:
“The greatest lurking danger for a user today is that many out-of-date and inferior methods remain in general use. Here are some traps to watch for:
- Never use a generator principally based on a linear congruential generator (LCG) or a multiplicative linear congruential generator (MLCG). We say more about this below.
- Never use a generator with a period less than ~ 264 ≈ 2 x 1019, or any generator whose period is undisclosed.
- Never use a generator that warns against using its low-order bits as being completely random. That was good advice once, but it now indicates an obsolete algorithm (usually a LCG).
- Never use the built-in generators in the C and C++ languages, especially rand and srand. These have no standard implementation and are often badly flawed.
If all scientific papers whose results are in doubt because of one or more of the above traps were to disappear from library shelves, there would be a gap on each shelf about as big as your fist.
You may also want to watch for indications that a generator is overengineered, and therefore wasteful of resources:
- Avoid generators that take more than (say) two dozen arithmetic or logical operations to generate a 64-bit integer or double precision floating result.
- Avoid using generators (over-)designed for serious cryptographic use.
- Avoid using generators with period > 10100. You really will never need it, and, above some minimum bound, the period of a generator has little to do with its quality.
Since we have told you what to avoid from the past, we should immediately follow with the received wisdom of the present:
An acceptable random generator must combine at least two (ideally, unrelated) methods. The methods combined should evolve independently and share no state. The combination should be by simple operations that do not produce results less random than their operands.”
244. And then the authors give what they say is a reliable generator.
245. Not only does this deprecate LCGs, Optis submitted, but it says that an “acceptable” random number generator must combine at least two methods.
246. At the end of page 344, NRC says this:
“Looking back, it seems clear that the field's long preoccupation with LCGs was somewhat misguided. There is no technological reason that the better, non-LCG, generators of the last decade could not have been discovered decades earlier, nor any reason that the impossible dream of an elegant "single algorithm" generator could not also have been abandoned much earlier (in favor of the more pragmatic patchwork in combined generators). As we will explain below, LCGs and MLCGs can still be useful, but only in carefully controlled situations, and with due attention to their manifest weaknesses.”
247. Optis submits that the last sentence only condones LCGs in the controlled situations referred to, and in combination with another method.
248. On the other hand, it was clear from Prof Lozano’s evidence, accepted by Ms Dwyer and also supported by NRC and Knuth (and Wikipedia for what it is worth) that LCGs were very well known, had a long history, and were fast and easy to understand and implement.
249. Ms Dwyer disagreed that any of NRC or Knuth or Wikipedia was CGK, but she did agree that if the skilled person wanted to use a RNG they would look it up and come across LCGs as one of the categories (and as I have said, she accepted Wikipedia as a jumping off point). She accepted that if the skilled person looked them up, they would find out:
i) The basic formula;
ii) The parameters;
iii) The sensitivity of the LCG to the choice of parameters;
iv) That LCGs were easy to implement and fast and that the theory behind them was easy to understand.
250. Drawing this together, the skilled person would appreciate from routine research that they would undertake if they considered that the Ericsson function should be replaced, that LCGs had much to commend them, and had been widely used for a long time. The skilled person would see Knuth as a reliable source of the teaching about how to implement LCGs that I have identified above in the section dealing with the teaching of Knuth.
251. The potentially very large “but” in Apple’s way lies in the comments in NRC that LCGs were actually poor, or even very poor random number generators, and should not be used on their own. Optis deployed this heavily.
252. Although initially very striking, I think the statements in NRC are of low relevance, at most, to the issue of obviousness in this case. I accept Prof Lozano’s evidence that what is under consideration in NRC is demanding situations where very long sequences of very random numbers are needed (“very random” in the sense that they pass extremely stringent tests intended to identify even the smallest signs of a pattern; an example was called “Diehard”). He was clear that sometimes sequences as long as 1030 or 1040 were needed, and that for cryptography sequences were needed and were produced that were “longer than the [age] of the universe measured in seconds”, but that that was “way beyond what anyone at RAN1 would even think about. At RAN1 we have never seen sequences of more than a few thousand or maybe tens of thousands of repetition of period.” He said that the more sophisticated RNGs in NRC were “way beyond anything that is required in a mobile device”.
253. Accordingly I think the skilled person’s attitude to LCGs would be that they were well known, widely used for a long time, easy to implement and suitable for low power devices, but not of good enough randomness for demanding applications. As with the recursive/self-contained debate which I have dealt with under the heading of CGK, the secondary evidence is consistent with my conclusion, but not necessary to it. Daewon Lee, the inventor, told RAN1 that what was proposed was “nothing new really”, that LCGs were “well studied” and that the idea was to “use what is well known equation as it is to achieve good randomisation properties”. Superficially this may seem to be really helpful to Apple, but without knowing more about the author’s characteristics and thinking it is of modest utility to my decision making. And of course his motivation may have been to reassure, having had the idea of using an LCG, that implementation of it would be smooth. That would not be inconsistent with the idea of using it having required insight.
254. Bringing this understanding to bear on the problem presented by Ericsson, the skilled person would know that there were about 65,000 UEIDs that needed to be distributed randomly, and that that was vastly lower than the scales relevant to cryptography etc. The skilled person would readily understand that LCGs were unsuitable if very large sequences of very random numbers were needed, but that that was not the relevant requirement for the PDCCH.
255. Prof Lozano explained this cogently in his written and oral evidence. In his second report, dealing with Ms Dwyer’s evidence (in the context of the specified claims) that the skilled person would think that a very long period for an LCG would be needed to give “the maximum amount of randomness”, he said:
“38. In any event, I do not think the skilled person would approach matters with the philosophy that paragraph 346 [of Dwyer 3] suggests. The problem in hand requires a number between 0 and 95 [the maximum value of C being 96], generated from a seed of between 1 and 65535. That requires 216 different randomisation patterns and of course the skilled person could generate random numbers a thousand digits long, but it would not be any more useful, and would be a lot more complicated, than generating what was actually needed. The skilled person would consider it unhelpful to work with larger numbers than are necessary for reasons of computational simplicity (see paragraphs 216 and 319 of my First Report).”
256. And he maintained this in cross-examination.
257. For all these reasons, I do not think there was a relevant “prejudice” against LCGs. The skilled person would think they were adequate for appropriately chosen tasks. As to the “lion in the path argument”, I would hold that the Patent does not change this perception one way or another. It contains a modest and rather poorly documented body of work showing that the use of an LCG gave acceptable results in an undemanding context.
Points raised by Optis
258. As well as attacking Apple’s case, Optis raised a number of positive points of its own. I will work through these, and where appropriate I devote specific sections to them, but they overlap so it is not possible to divide them entirely cleanly.
259. Optis said that there were other options than looking for RNGs in the way Apple put forward. Optis said that the skilled person might (or even would) look in books or book chapters about hashing functions not RNGs (such as the part of volume 3 of Knuth to which I have referred above). This argument depended quite heavily on the proposition that hashing and random number generation are entirely distinct, which I have rejected, but even if it is true that other functions might be identified, I think LCGs would still stand out as the best known and most used, for all that they had turned out to be unsuitable for demanding situations. I go into more detail in relation to “alternative routes” below.
260. As well as saying that there were other alternatives Optis put forward arguments that using an LCG involved a conceptual leap.
261. The first was that it was unknown to use a recursive solution in a hashing function, and that it was unknown to have different users starting at different points in the same sequence. Prof Lozano did not accept either point as having force. I have dealt above with why the recursive/self-contained distinction is not significant. As to different users starting at different places in the same sequence, that is just inherent to RNGs having a period.
262. The second was that it was unknown to use an RNG within a hashing function. I was unclear whether this was run as a separate point from the first or just a facet of it, but they are certainly related. I reject the point because the Ericsson function itself, which is clearly a hashing function, while not explicitly expressing its teaching in terms of an RNG, used what the skilled person would recognise as a source of randomness (Kx + L), coupled with the mod C operation. It was also known, and taught in Knuth, to take only part of a large random number generated by an LCG by various means which included taking the least significant bits using the mod function, and this is essentially hashing. I discuss this below in the next section, “A specific point on mod C”, and in relation to the specified claims.
263. The third conceptual leap point was what Optis called “horizontal v vertical randomisation”, with vertical randomisation being within a subframe and horizontal randomisation being between subframes. The point sought to be made was that Ericsson aimed to reconfigure the distribution systematically in each subframe (by changing x), and that it was hindsight to do that reconfiguration in a random way (with the LCG). Quite apart from anything else, the Ericsson function did not work and its failure was related to how it allowed repeated collisions in successive subframes, so I cannot see how the skilled person would form the impression that that was something to retain. But in any event I did not think Counsel for Optis made any progress with Prof Lozano on the point, and it was not one developed by Ms Dwyer in her written evidence, with Optis merely relying on some passing comments in the course of her cross-examination which I did not find clear or cogent.
264. More broadly, I think these conceptual leap arguments were attempts to put forward unrealistically abstract conceptions, when the skilled person would have a much more pragmatic approach.
265. Optis also ran an argument that if the skilled person had the idea of an LCG they could turn the Ericsson function into an LCG in the form Startk = (K*Startk-1 + L) mod C. Ms Dwyer had suggested this in her fourth report at paragraph 113, expressed very slightly differently, with Start-1 (she called it x-1) as either UE-ID*16 + subframe number or UE-ID. But Prof Lozano had pointed out in response that the first of those was meaningless and the second would give extremely limited randomisation. Ms Dwyer had accepted those powerful criticisms so I do not see how the suggestion of changing Ericsson into an LCG by modification like this can be maintained.
266. This idea of modifying Ericsson in this way (which I have rejected) was linked by Optis to a discussion which emerged at trial about whether the Ericsson function was reminiscent of an LCG. As Prof Lozano pointed out, the Ericsson function has a modulus, a multiplier, an increment and a starting value, as does an LCG. It clearly is not in fact an LCG because it is not recursive, though. It is possible, I think, that the skilled person would see this conceptual similarity between the Ericsson function and LCGs, and they might even think that the Ericsson function was a botched effort at an LCG (the secondary evidence provides some support for the notion), but I do not think it is important and would not significantly affect what the skilled person would do.
267. Overall therefore, I do not think that Optis’ points thus far undermine my view that using an LCG would be an obvious thing for the skilled person to do, based on a literature search.
A specific point on mod C
268. Optis argued that even if it was obvious to replace the Kx + L part of the Ericsson function with an LCG, it would not be obvious to use mod C to convert the result of the LCG to a value between 0 and C-1, because the use of mod C would take the low order (right hand) bits of the LCG output, and those would be less random. The alternative is to convert the output of the LCG to a number between 0 and 1 by dividing by the modulus of the LCG, multiplying by C, and taking the integer part.
269. This is related to the points on the specified claims. Knuth explains at 3.2.1.1 that the problem of low-randomness right hand bits arises in particular with a modulus that is a power of 2, and is avoided with a modulus which is prime, and of the form 2n±1. So the skilled person who had read Knuth would not think that there was any general problem with using mod C, provided care was taken.
270. In oral evidence Prof Lozano said that using mod C to scale a larger number down was the usual approach of 3GPP. Ms Dwyer said that she did not know what the normal 3GPP approach was, but that the two alternatives were two ways of doing the same thing. I do not think they are simple alternatives, in fact, because clearly there are instances where using mod C is suboptimal, but in any event overall I prefer Prof Lozano’s evidence, and I reject this point by Optis. It is a slightly odd one in any event because clearly the authors of Ericsson were advocating using mod C to scale down the output of Kx+L without any attempt to verify that the low order bits were random.
Use of max hits
271. Moving on from the question of whether a function as used in the claims of the Patent would be one obvious option, Optis argued that the metric of max hits was not CGK and that there had been invention in using it to verify the suitability of the function as a workable alternative to Ericsson.
272. There is a strong flavour of “parametritis” about this argument. Parametritis is an expression used in a number of contexts and it can take a number of forms. One is where a claim specifies what it covers by reference to a parameter which has never been used before; since it has never been used before it is impossible for the claim to be anticipated and obviousness arguments are met by the patentee saying that it was not obvious to use that parameter. See the discussion by Laddie J in Bourns v. Raychem (No 2) [1998] RPC 31. It is especially pertinent where achieving the parameter does not reflect any useful result.
273. Optis relies on max hits even though it is not in the claims; it argues that using it to progress Ericsson would be a sign of invention because it was not CGK and the skilled person would have to think of it themselves.
274. In the present case, Prof Lozano agreed that max hits was not a CGK parameter, but he put it forward as something the skilled person would do in progressing Ericsson. However, he thought it was not a very meaningful parameter, at least on its own, because it may just mean that in a generally well-functioning system there are very rare occasions when two UEs collide for all ten subframes. He called this “anecdotal”.
275. Since the problems with Ericsson that would lead the skilled person to change its function included repeated collisions over many subframes, I think it would be entirely natural for the skilled person to look at the maximum collisions arising from a modified function, as a part of their work. But they would not see it as a big contributor to the analysis. Ms Dwyer accepted at least in relation to the specified claims that testing for max hits would be a sensible metric.
276. In any event, the max hits point is a minor one. It is not necessary for Apple’s case to identify with absolute precision what simulations the skilled person would do. They would do an appropriate and adequate mix and would have the ability to devise it.
Same parameters for all aggregation levels
277. In principle one might have different parameters for different aggregation levels. Prof Lozano said that the additional complexity would not be warranted and this was not challenged in cross-examination. Ms Dwyer accepted that using the same parameters for each aggregation level would be the simpler choice, but she did not accept it was the best. Optis relied on this only weakly. I again prefer Prof Lozano’s position.
Assessment of the secondary evidence
278. I have set out the law in relation to secondary evidence above. It must be kept in its place. If it has a value, it is to help the Court assess the primary question of how the ordinary, uninventive skilled person would behave. The skilled person is completely uninventive but exceptionally diligent.
279. As I have already said, the secondary evidence in this case has the advantage that all the workers had in mind very specifically the cited prior art, Ericsson. That certainly assists its potential relevance, but it leaves open the question of the extent to which the people concerned approximated to the skilled person in the respects I have just mentioned.
280. In this section of this judgment I will give my overall views about the secondary evidence. I picked up some individual points above as they arose, with these broader considerations in mind.
281. A great deal of material was provided in relation to the secondary evidence. There were four files of documents, split into two pre- and two post-priority. The experts put in extensive evidence, especially Ms Dwyer.
282. However, I did not receive any witness statements from any of the workers in question. Counsel for Optis rather optimistically submitted that I should hold it against Apple that they had failed to lead any evidence from the workers, but I reject this as there is no reason to think that Apple was in a position to get such evidence. If anything, it would have been Optis that bore an onus to do this, as the party primarily advancing secondary evidence and as the successor in title to the original patentee. But I have no positive reason to think that Optis would have been able to do that either. The lack of evidence from the workers is a limitation on the utility of the secondary evidence but not to be laid at the door of either of the parties.
283. There were too many documents to hope to cover them all at trial, and understandably the cross-examination focused on a subset. I directed that the parties should prepare a chronology that listed the documents and highlighted the ones that received emphasis at trial. I am grateful for the very useful chart that emerged and I have re-read the main documents with its guidance.
284. The documents mainly relied on date back to January 2008 with what was called “Samsung I”, then cover the provision of what was called the “kick-off” email from Stephan Parkvall of Ericsson on 30 January 2008, Ericsson itself on 15 February 2008, a flurry of activity on 26 to 30 March 2008, and another set of contributions on 4 April 2008, with the adoption of the solution of the Patents also on 4 April 2008. As I have said, this period spans the priority date and the documents include comments made prior to knowing of the proposal that became the Patents, and comments upon that proposal once made.
285. The evidence focused on comments by, and/or work from, the following:
i) Samsung.
ii) Ericsson.
iii) Motorola.
iv) Nokia.
v) Qualcomm.
vi) LGE.
vii) Philips.
viii) NTT DoCoMo.
286. I make the following general findings:
i) I cannot be at all confident that the individuals concerned approximated in their capabilities to the ordinary skilled person. They probably did not, in the sense that they were likely to be exceptionally skilled.
ii) The objectives of the individuals concerned included finding a good, and perhaps the best, technical solution, but also included advocating and having adopted solutions in relation to which they could get, or already had, patents. Qualcomm had a position in Gold codes, as I have already mentioned.
iii) Many of the key discussions happened in an extremely short timeframe. There were multiple communications within a few hours on 26 March 2008, to such an extent that untangling the sequence involves careful consideration of the time zones in which the participants were.
iv) There is as a result an overall sense of haste which I think leads to a very poor approximation of the careful and steady approach to be expected of the notional skilled person. The discussions are a sort of email-mediated, multi-company brainstorming session. No doubt those involved also had many other tasks to do at the same time.
v) On top of the haste for individual contributions, overall the period from the availability of Ericsson to the making of the invention and thereafter to its adoption by RAN1 is a very short one. So Optis’ “why was it not done before” point does not work at all well.
vi) The specific contributions in papers submitted by workers at companies among those listed above are very varied.
vii) Some of the contributors (Nokia, NTT) made mistakes which the notional skilled person would not have.
287. The variation among the contributions mean that there is something for Optis and something for Apple to be found among them. Some contributors realised there was a problem of repeated collisions across subframes (which could favour Apple) and others did not (which could favour Optis). Some proposed that Ericsson was actually overengineered, and that too could favour Optis, and Optis also put stress on Motorola doing simulations (Prof Lozano thought they were the best done) and not identifying the lockstep problem from them. However, I do not find these sorts of points helpful in the absence of being able to rely on the contributors being representative of the notional skilled person, and without knowing in detail what they had done, and why.
288. I do think some very general trends emerge:
i) There is fairly frequent reference to randomness as well as to hashing. This supports Apple’s case that there is no bright line between the concepts.
ii) There is no sense that the degree of randomness needed was of the order that would be required for cryptography or the like. The focus was on finding a function which achieved enough randomness for the task in hand.
289. If anything, these tend to favour Apple.
290. Overall, in the face of the limitations that I have explained, I consider that LGE itself probably best represented the approach of the ordinary skilled person. It thought carefully about Ericsson and whether it would work and if not then why not, it did some calculations/simulations, and it advocated going with an established, known kind of simple but adequate function in the form of the LCG (by contrast with other contributors who were proposing new functions). It was focused on the practicalities of the concrete situation when it met the recursive/self-contained concern by pointing out that the calculation load actually required was small. I am conscious that it is circular and unfair to say that just because the patentee made the invention it must be obvious, but here I have a greater than usual, albeit incomplete, understanding of the route taken and am able to conclude that it matches what the ordinary addressee would do quite well.
291. I am confident, in any event, that the secondary evidence does not militate against a conclusion that one obvious route forward from Ericsson was to use an LCG, and it is nowhere near enough to displace what I have found is a clear picture from the primary evidence.
Alternative routes - overall assessment
292. I have already mentioned possible alternative routes in a number of places. My overall assessment is that:
i) A variety of ways of changing the Ericsson function could be considered, and at least some would occur to the skilled person. But given that the Ericsson function had failed in a number of ways and was somewhat uncharted territory (in the sense that Kx + L was not a known random number generation/hashing approach) they would not be very attractive. Prof Lozano said, and I accept, that the skilled person would think that changing x might solve some of the problems, but not all.
ii) Changing Ericsson so as to make it an actual LCG (i.e. without nested mod operations) would not be at all attractive or clear as a way forward.
iii) Some of the suggestions made (e.g. Qualcomm, Samsung) involved the provision of self-contained functions. Qualcomm used the well-known Gold codes and Samsung used a cyclically-shifted x. These are possible alternatives but they are not necessarily against Apple’s case because they retain mod C and support the overall approach of getting rid of the Ericsson function instead of tweaking it.
iv) In conducting the literature search referred to above the skilled person would come across other known hashing/randomisation functions (for example the ones identified by name in Wikipedia/NRC, or the specific options set out in NRC), and although I have rejected the hashing/RNG distinction urged by Optis I agreed that the skilled person would look in the hashing sections of relevant works. These would certainly be worth considering and could have the advantage of very reliably providing a high degree of randomness, but at the potential cost of implementation complexity and calculation intensiveness.
v) If the skilled person opted for, or was actively considering, an LCG then they would see the suggestions about how to do that in NRC and other parts of Knuth, including possibly the recommendation made in the summary in Knuth. This has more relevance to the unspecified claims.
293. Even taking these as a whole, they do not lead me to doubt my view on obviousness. There were certainly other options, but the fact that LCGs were so well known and understood, and still known to be useful where the randomness needed was not too great, mean that they would be at the very least a leading option.
Conclusion on obviousness of the unspecified claims from Ericsson
294. I accept Apple’s case. The problem with the Ericsson function would be identified readily and by routine analysis. It would be clear without invention that the mod C part of the function was all right and the Kx + L needed remedy. A literature search would readily throw up LCGs as the best known option and although they would be known to have limitations they would be regarded as adequate for the PDCCH task in hand.
295. The secondary evidence does not displace this conclusion and nor do the existence of other alternatives; in any event an LCG would be at the forefront of any list of options.
296. In reaching this conclusion I have borne very much in mind that Apple’s case involves a number of sequential steps. But I find that they represent systematic uninventive work and not the use of inappropriate hindsight.
Obviousness of the specified claims
297. The specified claims add requirements as to A, B and D. Claim 4 of the Patent requires that D (the modulus) is 65537, that A (the multiplier) is 39827, and that B (the increment) is 0.
298. I will deal with this in the order B, D, A (m, c, a in Knuth’s terminology); I have to deal with them in some order, but I do not lose sight of the fact that they are related.
299. There was no material dispute that the natural seed to use was the UEID, being a number known to the network and the UE.
300. One option for the skilled person would be to use what Knuth suggests in his summary, but I do not think that that would be the only option by any means and I do not think it would dissuade the skilled person from thinking about values specifically suitable for the PDCCH situation, which is how Apple advanced its case through the evidence of Prof Lozano.
B (increment) as 0
301. As I have explained in dealing with the disclosure of Knuth, B = 0 was a known useful category (“multiplicative”) of LCGs and Optis put little effort into defending it as being inventive in itself. I find that if the skilled person had followed the route to claim 1 argued for by Apple (as I have held they would) then B = 0 would be one obvious option, and probably the most obvious option, since it simplifies things and can be achieved without material loss of period/randomness if certain rules are followed.
D (modulus) as 65537
302. This was the point of greatest debate on the specified claims. There are a number of related strands to it.
303. One point was that a modulus of 65537 is, Optis said, much too small and therefore not obvious to choose. Optis said it was much too small because of the advice in e.g. Knuth to make the period (which cannot exceed the modulus) very big, and much bigger than the number of sequence elements to be used. But, Optis pointed out, 65537 is only a tiny bit bigger than the number of UEIDs (65535).
304. Prof Lozano said that 65537 was a good and sensible number to choose because it was:
i) In the form 2n+1, it being known from Knuth that 2n, 2n-1 and 2n+1 were beneficial for ease of calculation, but with 2n giving much less randomness in the rightmost (least significant) digits.
ii) Prime, and therefore able to be prime relative to A, so as to maximise the period.
iii) Just big enough to give one result per possible UEID if the period was maximised. He said that as a general matter making it smaller would make calculations easier, which I accept
305. And he noted that 65537 appears in the table on page 13 of Knuth as being 216+1, and prime (since no factors are shown for it). 216-1 would also make calculations easier, but it is not prime (the table shows that it is 3x5x17x257) and that would be a limitation when choosing a multiplier.
306. Optis disputed all of this.
307. As to the form 2n+1, Optis submitted that that only applied where 2n was the computer’s word size (“w”), which would not be true for 65537 (for a 32 bit computer such as was in use at the priority date in mobile devices). However, Prof Lozano disagreed that the teaching in that part of Knuth was so limited; it does refer to the computer word size because (he said) Knuth is a book about computer programming, but the ease of calculation advantage is not tied to computer word size. He also pointed out that it was not sensible to tie the choice of parameter to word size in LTE because it would change as better processors came to be used.
308. I accept that evidence, and I also accept his evidence as to the explanation bridging pages 12 to 14 that randomness of the rightmost digits would be preserved by using 2n+1.
309. The explanation as to knowing the prime factors of the modulus to choose the multiplier correctly is contained in the paragraph lower down page 12 beginning “In later sections …”.
310. Prof Lozano was pressed hardest on the proposition that a much larger modulus than 65537 would be thought to be needed, based on the numerous general statements in Knuth that a large modulus was appropriate, to give a period containing far more numbers than would ever be used. He was firm that in the context of LTE there was no point generating far more numbers than were needed, and that it would add to the calculation load to do so. I accept this and it gels with my findings on the CGK that the amount of randomness needed must depend on the application. The skilled person would think that 65537 was very likely to be adequate, and would know that they could assess its suitability with calculations/simulations, to see if it achieved the practical task of keeping collisions to a tolerable level.
311. Ms Dwyer disagreed in her written evidence with the choice of 65537 being an obvious one, but she did accept in cross-examination that:
i) The period should not be less than 65535. This agreement did not take matters far because the argument was about whether or not to go (a lot) higher.
ii) The design for LTE would not be based on computer word size.
iii) Knowing the prime factors of the modulus would be relevant to choosing the multiplier in due course. She accepted that page 19 taught that where the increment was 0, the period would be effectively maximised (actually equal to the modulus minus 1) if the modulus was prime. This is one reason why the various choices are related.
312. In her written evidence she had said that 65537 was surprisingly small, but she made little of it in her oral evidence.
313. Eventually she agreed that when asked if 65537 was a “sensible choice” that “It is one choice. I would not say it is the best one”, that it was “above the number of UEIDs, which we said was important, and it is a prime number. It is not the only prime number above that. It is not the only prime number that is word size +/- 1 either”.
314. This was very close indeed to accepting that 65537 was a sensible choice. Weighing this along with Prof Lozano’s evidence I prefer the latter to the extent there was a difference, which there barely was. 65537 was an obvious choice and indeed probably the most obvious choice since it stands out so clearly from the table on page 13 once one understands the appropriate thinking.
A (multiplier) as 39827
315. A multiplier of 39827 is an adequate choice to combine with a modulus of 65537; it is not the best and Prof Lozano showed that there are many other numbers that are (slightly) better. So it is not an arbitrary choice, but nor is it by any means outstanding. Ms Dwyer’s evidence was consistent with this.
316. Prof Lozano said that 39827 was one of a number of values which would work, and could be identified by routine simulations. Ms Dwyer agreed that the skilled person, given their decision on the modulus, would proceed by simulations.
317. Prof Lozano mentioned the use of “max hits” in the course of describing the kind of simulations that would be used. Building on that, Optis argued that since max hits was not a CGK parameter, it would be inventive to do the simulations that Prof Lozano had in mind. I have explained above why I was unimpressed with max hits generally, but in any event I think it is an unfair appreciation of Prof Lozano’s evidence as a whole that he thought max hits was an essential element of what to look at. The broader thrust was that simulations generally would yield adequate values for the multiplier.
318. In any event, Prof Lozano also said that it would be obvious to choose a multiplier which maximised period length. For a modulus of 65537, a multiplier of 39827 does this. Optis pointed out that he only mentioned this in his third report. That is true, and it has somewhat less weight as a result, but it makes sense and further supports his analysis.
319. Moreover, Knuth provides analytical ways to identify good multipliers: they should be primitive elements modulo D (modulo m for Knuth). This is explained at pages 19-20 of Knuth. Ms Dwyer had said that that was too difficult to understand. Prof Lozano did not agree, although the sense of his evidence was that proceeding by calculation/simulation was more practical. In any event, the availability of a theoretical approach that could be followed if necessary further supports it being obvious to get to 39827.
320. I therefore conclude that 39827 was an obvious option to adopt.
321. Thus each value in claim 4 is at least an obvious value. Although I have had to explain my reasoning in a sequence of steps I am satisfied there is no improper salami-slicing. Each step flows into the next for logical and routine reasons. The choices are related in ways which support their combination being obvious. This is basically careful implementation work of the kind for which the notional skilled person is inherently well-equipped, and this was part of the case where I thought Prof Lozano’s advantage over Ms Dwyer was particularly striking. Claim 4 is obvious.
Obviousness over Knuth
322. This was Apple’s secondary case. As I understood Counsel for Apple’s submissions it could only succeed where Ericsson failed if the skilled person starting from Ericsson would not find their way to Knuth at all. Starting from Knuth by taking it as a specific prior art citation would ensure, as a matter of law, that the skilled person had it and read it with interest. If they then were apprised of Ericsson and all that flowed from that, the argument would be the same, with the same ingredients, as starting from Ericsson.
323. Because I have found that the obviousness case over Ericsson succeeds, I will deal with this alternative only briefly.
324. Since it requires that the skilled person gets Ericsson, and since there is of course no cross-reference from Knuth to Ericsson, the argument needs Ericsson to be CGK. Apple said that it would be CGK if the skilled person were the PDCCH person. I have rejected that, so the argument fails at the outset.
325. In any event, I found the argument very artificial and therefore unpersuasive.
326. The case starting from Ericsson has a goal (PDCCH search space allocation), a suggestion (the Ericsson function), a concrete problem which would be apparent on routine analysis (the deficiency in the function) and then the application, with appropriate implementation details, of a CGK solution (LCGs as taught in Knuth).
327. By contrast, the case starting from Knuth involves giving the skilled person a bag of solutions and inviting him or her to go and find problems on which to use them. It is worse than that, however, because it involves using the tools provided in Knuth in a particular combination, not just using something that is presented in Knuth as a ready-to-go solution.
328. I accept that there could be cases where it would be obvious to take a specific tool or solution and apply it to known tasks or types of tasks for which it was clearly suitable, perhaps quite a lot of different tasks, in the sense that a new glue might obviously be going to work on anything broken. But that is not this case. The direction of travel is all wrong.
329. I therefore reject the case starting from Knuth.
Insufficiency
330. There are two allegations of insufficiency; one against the unspecified claims and one against the specified claims
Insufficiency of the unspecified claims
331. The allegation is that the unspecified claims include functions that produce a very high number of persistent hits. Prof Lozano gave six examples in his first report. They included (these three examples were given in Apple’s written submissions):
i) Where A = D, in which case there will be 10 hits for all values of C for all UEID pairs;
ii) D<65535, when max hits will be 10 for all values of C for UEIDs greater than D;
iii) D is not prime, which will frequently give 10 hits for values of C where C and D are not relatively prime.
332. Prof Lozano was not challenged on this evidence and I understood it to be to the effect that in these situations the number of hits was bad enough to render the patented function lacking in practical usefulness.
333. Optis’ opening skeleton suggested that such high number of hits did not necessarily mean that the function would not work, since collisions are not the same as blocking. I accept this, but if it were to be Optis’ case that Prof Lozano’s examples were all just instances of collisions and not blocking then it was incumbent on them to put that to the professor, and they did not.
334. In closing written submissions, Optis sought to engage with the three examples given above (but said nothing about the professor’s other examples). It said that they were obviously absurd or easily addressed, but again this should have been put if it was to be run (although I tend to agree that A = D is plainly a silly thing to do).
335. So I would conclude that the unspecified claims cover combinations of parameters which are so bad that it can meaningfully be said that they do not work at all (how many such combinations there are was not really addressed, but Apple did not seek to prove that they were very numerous, or a significant proportion of the total possibilities and my sense is that there was a non-trivial number but only a small proportion of the total). In my view, however, that does not make the claim insufficient as long as the skilled person would be able, using their CGK, to identify and avoid the bad combinations without undue effort, and pick working combinations appropriate to their requirements without undue effort - the situation is very like the Markush group in FibroGen v. Akebia [2021] EWCA Civ 1279 where the skilled person could find useful compounds across the scope of the claim by routine (though hard) work.
336. Apple essentially recognised that this was a way out of the insufficiency allegation for Optis; that is why this attack was positioned as a squeeze against the specified claims, with Apple saying that if the skilled person could identify working combinations of parameters without undue effort then they must be able to bring the same aptitude to bear on the specified claims. I asked Counsel for Optis how Optis reconciled this. The argument in response was that the Patent improved the position of the skilled person in that it gave examples of simulations that could be done, and teaching in e.g. paragraphs [107]-[108], to which I have referred above. But I think the simulations are nothing that the skilled person would not be able to do from the CGK (and Tables 3 and 4 require work to make sense of, at the least), and [107]-[108] just present information from those simulations and/or that can readily be found in Knuth in a more comprehensible and accurate, and less confusing form.
337. My conclusion is that this allegation fails to render the specified claims insufficient, but only because the skilled person has a significantly higher degree of aptitude than Optis argued for when defending the inventiveness of the specified claims, and could root out bad combinations and choose good ones using their CGK. In other words, the allegation is an effective squeeze insofar as it pushes the abilities of the skilled person towards a level which helps Apple. To be clear, however, the squeeze is not necessary to my conclusions of obviousness, as I found the skilled person to have the characteristics and CGK referred to above prior to taking the squeeze into account.
The specified claims
338. This allegation focuses on the value of the multiplier A as 39827. Apple pointed out that Optis claims 39827 is useful in that it “works”, and indeed performs better than some other possibilities. Apple said that that is a technical benefit and must be rendered plausible by the specification or otherwise the patent is insufficient, with a bare assertion not being good enough. It cited Eli Lilly v. Genentech [2019] EWHC 387 (Pat) at [528]. Then Apple said that the teaching of the Patent in relation to Tables 3 and 4 is too defective, as I have touched on above, to render plausible the proposition that A = 39827 is useful.
339. It seems to me that this is at most an allegation that A = 39827 is an arbitrary value. Birss J held in Optis v. Apple (Trial A) [2020] EWHC at [207]-[208] that merely having an arbitrary feature in a claim is not a ground of invalidity (he was upheld on obviousness on appeal, including on this point, although the Court of Appeal’s decision was not available at the time of the trial before me). His statement was made in relation to Agrevo obviousness, but I do not think he would have said it if having an arbitrary feature in itself led to insufficiency; Agrevo obviousness and insufficiency are intimately related.
340. Even if A = 39827 were a merely arbitrary choice among the multipliers compatible with making the best use of a modulus of 65537, the modulus provides a useful technical contribution. So this is not a case where there is no technical contribution at all (cf. Optis v. Apple (Trial A) at [208] last sentence). Of course, I have found both parameters to be classically obvious.
341. Since I consider that A = 39827 being arbitrary would not on its own invalidate the claim, I do not need to consider if the utility of that value is rendered plausible, but I will briefly do so.
342. Plausibility is a low threshold. I do not see that even that low threshold can be met by the mere inclusion in Table 4 of an entry for A = 39827 and D = 65537; that is bare assertion. However, a value for max hits is given, and that is some data tending to show that the combination is useful. If the skilled person dug into the numbers they would find that something was not quite right, for reasons given by Prof Lozano and partly accepted by Ms Dwyer. But having started down that route, the skilled person would probably also see that the max hits column did make sense for C = 16. In my view this provides just enough to show that A = 38927 had some utility. But at the same time it requires an aptitude and perceptiveness on the part of the skilled person that fits poorly with what Optis argued for on obviousness.
343. Optis also relied on the possibility that the skilled person could use mathematics to justify the conclusion that A = 39827. That is true, but it is in tension with Optis’ position on the obviousness of A = 39827, even allowing for the fact that the obviousness question is about deriving A without knowing it in advance, and the insufficiency question is about verifying its utility.
344. So I reject this insufficiency as well.
Conclusions
345. My conclusions are:
i) The Patents, as to all the claims in issue, are all obvious over Ericsson.
ii) The obviousness case starting from Knuth fails.
iii) The insufficiency allegations fail.
346. I will hear Counsel as to the form of Order if it cannot be agreed. I direct that time for seeking permission to appeal shall not run until after the hearing on the form of Order (or the making of such Order if it is agreed).
