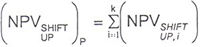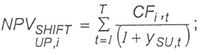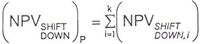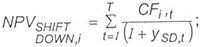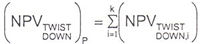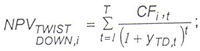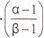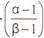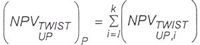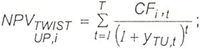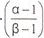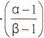S.I. No. 386/2002 -- Asset Covered Securities Act, 2001 (Section 91(1)) (Sensitivity To Interest Rate Changes) Regulation, 2002
|
ASSET COVERED SECURITIES ACT, 2001 (SECTION 91(1)) (SENSITIVITY TO INTEREST RATE CHANGES) REGULATION, 2002 |
||||||||
|
ASSET COVERED SECURITIES ACT, 2001 (SECTION 91(1)) |
||||||||
|
(SENSITIVITY TO INTEREST RATE CHANGES) |
||||||||
|
REGULATION, 2002 |
||||||||
|
The Central Bank of Ireland (the “Authority”), in exercise of the powers conferred on it by Section 91(1) of the Asset Covered Securities Act, 2001 (No. 47 of 2001) , hereby makes the following Regulation: 1. This Regulation may be called the Asset Covered Securities Act, 2001 (Section 91 (1)) (Sensitivity to interest Rate Changes) Regulation, 2002. 2. In this Regulation the “Act” means the Asset Covered Securities Act, 2001 (No. 47 of 2001) . A word or expression that is used in this Regulation and is also used in the Act has, unless the contrary intention appears, the same meaning in this Regulation as in the Act. 3. Measurement of sensitivity to interest rate changes shall be determined as follows |
||||||||
|
(a) Sensitivity to interest rate changes shall be calculated using net present value changes based on:- |
||||||||
|
One hundred basis points upward shift in the yield curve |
||||||||
|
One hundred basis points downward shift in the yield curve and |
||||||||
|
One hundred basis points twist in the yield curve. |
||||||||
|
(b) All calculations of sensitivity to interest rate changes are to be carried out in accordance with the formulae set out in the Schedule to this Regulation. |
||||||||
|
(c) All positions sensitive to changes in interest rates (whether in the cover-assets pool or not), but excluding capital, should be included in the measurement. 4. Net present value changes arising from any of the scenarios above shall not exceed 10% of the designated public credit institution's total own funds at any time. |
||||||||
|
||||||||
|
EXPLANATORY NOTE |
||||||||
|
(This note is not part of the Instrument and does not purport to be a legal interpretation.) |
||||||||
|
This Regulation prescribes formulae for calculation of sensitivity to interest rate changes for designated public credit institutions. |
||||||||
|
SCHEDULE FORMULAE IN RESPECT OF SECTION 91(1) (SENSITIVITY TO INTEREST RATE CHANGES) REGULATION |
||||||||
|
This schedule sets out the formulae to be used by designated public credit institutions in measuring sensitivity to interest rate changes. |
||||||||
|
1. Calculation of Net Present Values |
||||||||
|
1.1 Fixed Interest Rate Instruments |
||||||||
|
The net present value of a cover asset, cover asset hedge contract or security issued, the interest payable on which is fixed, is calculated as the sum of the present values of each cashflow payable on the instrument in each time period: |
||||||||
|
||||||||
|
where |
||||||||
|
CFt = Interestt + Capitalt |
||||||||
|
st is the zero coupon interest rate, at valuation, to time t |
||||||||
|
z is a static spread over the zero coupon interest rate that lets the net present value of the instrument be equal to its price. |
||||||||
|
1.2 Floating Interest Rate Instruments |
||||||||
|
The net present value of a cover asset, cover asset hedge contract or security issued, the interest payable on which is floating, is calculated as the sum of the present values of each cashflow payable on the instrument in each time period: |
||||||||
|
||||||||
|
where |
||||||||
|
CFt = Interestt + Capitalt; |
||||||||
|
st is the zero coupon interest rate, at valuation, to time t; and |
||||||||
|
x is a static spread over the zero coupon interest rate that lets the net present value of the instrument be equal to its price. |
||||||||
|
1.3 Net Present Value of Cover Asset Pool or Securities Issued |
||||||||
|
For the purposes of this regulation, the net present value of the cover asset pool or securities issued is calculated as the sum of the net present values of the instruments in the cover assets pool or the securities issued as the case may be. |
||||||||
|
2. Measurement of Sensitivity to Interest Rate Changes |
||||||||
|
Designated public credit institutions shall use the following methodology in measuring their sensitivity to changes in interest rates. |
||||||||
|
2.1 Upward Parallel Shift in the Yield Curve |
||||||||
|
For a one hundred basis points upward shift in the yield curve, the resultant net present value of the cover asset pool, securities issued or other positions sensitive to changes in interest rates shall be calculated as: |
||||||||
|
|
||||||||
|
where, for an individual cover asset or cover asset hedge contract, i: |
||||||||
|
|
||||||||
|
ysu,t = (St + z) + (0.01) for fixed rate instruments; |
||||||||
|
ysu,t = (st + x) + (0.01) for floating rate instruments; |
||||||||
|
St = zero coupon interest rate, at valuation to time t; |
||||||||
|
z is a static spread over the zero coupon interest rate that lets the net present value of the instrument be equal to its price; and |
||||||||
|
x is a static spread over the zero coupon interest rate that lets the net present value of the instrument be equal to its price. |
||||||||
|
2.2 Downward Parallel Shift in the Yield Curve |
||||||||
|
For a one hundred basis points downward shift in the yield curve, the resultant net present value of the cover asset pool, securities issued or other positions sensitive to changes in interest rates shall be calculated as: |
||||||||
|
|
||||||||
|
where, for an individual cover asset or cover asset hedge contract, i: |
||||||||
|
|
||||||||
|
ySD,t = (st + Z) - (0.01) for fixed rate instruments; |
||||||||
|
ySD,t = (st + X) - (0.01) for floating rate instruments; |
||||||||
|
st = zero coupon interest rate, at valuation, to time t, |
||||||||
|
z is a static spread over the zero coupon interest rate that lets the net present value of the instrument be equal to its price; and |
||||||||
|
x is a static spread over the zero coupon interest rate that lets the net present value of the instrument be equal to its price. |
||||||||
|
2.3 Changes in the Slope of the Yield Curve |
||||||||
|
2.3.1 General Approach |
||||||||
|
The procedure for the calculation of the net present value of the of the cover asset pool, securities issued or other positions sensitive to changes in interest rates resulting from a one hundred basis points twist in the yield curve is as follows: |
||||||||
|
• For all revaluation points along the yield curve up to and including 3 months (i.e. the ‘short end’), increase (decrease) the yield curve values by 100 basis points; |
||||||||
|
• For all revaluation points along the yield curve greater than or equal to 10 years (i.e. the ‘long end’), decrease (increase) the yield curve values by 100 basis points; and |
||||||||
|
• In the interval from 3 months to 10 years, make proportional changes to the yield curve in accordance with the number of revaluation points in the interval. |
||||||||
|
This new yield curve is then applied to all instruments in the cover asset pool, securities issued or other positions sensitive to changes in interest rates. The formulae for the calculation of the net present value of all instruments resulting from a one hundred basis points twist in the yield curve are set out in 2.3.2 and 2.3.3 below. |
||||||||
|
2.3.2 Downward Change in the Slope of the Yield Curve |
||||||||
|
For a twist in the yield curve, up one hundred basis points in the short term and down one hundred basis points in the long term, with proportional changes in the interval, the resultant net present value of the cover asset pool, securities issued or other positions sensitive to changes in interest rates shall be calculated as: |
||||||||
|
|
||||||||
|
where, for an individual cover asset or cover asset hedge contract, i: |
||||||||
|
|
||||||||
|
||||||||
|
||||||||
|
α,β ≤ 1 ; α,β € N ; |
||||||||
|
α = 1 for t ≥ 3 months; |
||||||||
|
α = β for t ≤ 10 years; |
||||||||
|
for 3 months ≥ t ≥ 10 years, assign ascending values of β to each revaluation point along the curve greater than 3 months and less than 10 years, beginning with α = 1 for t = 3 months; |
||||||||
|
β is the final revaluation point along the curve required in the interval (3 months ≥ t ≥ 10 years); |
||||||||
|
z is a static spread over the zero coupon interest rate that lets the net present value of the instrument be equal to its price; and |
||||||||
|
x is a static spread over the zero coupon interest rate that lets the net present value of the instrument be equal to its price. |
||||||||
|
2.3.3 Upward Change in the Slope of the Yield Curve |
||||||||
|
For a twist in the yield curve, down one hundred basis points in the short term and up one hundred basis points in the long term, with proportional changes in the interval, the resultant net present value of cover asset pool, securities issued or other positions sensitive to changes in interest rates shall be calculated as: |
||||||||
|
|
||||||||
|
where, for an individual cover asset or cover asset hedge contract, i: |
||||||||
|
|
||||||||
|
||||||||
|
||||||||
|
α, β ≤ 1; α,β € N ; |
||||||||
|
α = 1 for t ≥ 3 months; |
||||||||
|
α = β for t ≤ 10 years; |
||||||||
|
for 3 months ≥ t ≥ 10 years, assign ascending values of α to each revaluation point along the curve greater than 3 months and less than 10 years, beginning with α = 1 for t = 3 months; |
||||||||
|
β is the final revaluation point along the curve required in the interval (3 months ≥ t ≥ 10 years); |
||||||||
|
z is a static spread over the zero coupon interest rate that lets the net present value of the instrument be equal to its price; and |
||||||||
|
x is a static spread over the zero coupon interest rate that lets the net present value of the instrument be equal to its price. |
||||||||
|
2.4 Sensitivity to changes in interest rates |
||||||||
|
For the purposes of this Regulation, sensitivity to changes in interest rates is measured as the difference between: |
||||||||
|
• Actual net present value and the resultant net present value from a one hundred basis point upward shift in the yield curve; |
||||||||
|
• Actual net present value and the resultant net present value from a one hundred basis point downward shift in the yield curve; |
||||||||
|
• Actual net present value and the resultant net present value from a twist in the yield curve of plus one hundred basis points in the short term and minus one hundred basis points in the long term, with proportional changes in the interval; and |
||||||||
|
• Actual net present value and the resultant net present value from a twist in the yield curve of minus one hundred basis points in the short term and plus one hundred basis points in the long term, with proportional changes in the interval. |
||||||||
|
3. Euro-Swap Curve |
||||||||
|
For the purposes of this Regulation, the euro swap curve shall be used as the reference curve for valuing all cover assets, cover asset hedge contracts and securities issued. |

 GOVERNOR
GOVERNOR